Numerical Integration

GSL Shell has moved

The project, its documentation and the release packages are now hosted on Github. Please find here the user manual.

This chapter describes routines for performing numerical integration (quadrature) of a function in one dimension. GSL Shell re-implements the the algorithms used in QUADPACK, a numerical integration package written by Piessens, Doncker-Kapenga, Uberhuber and Kahaner. FORTRAN code for QUADPACK is available on Netlib.

Currently only two integration methods are available in GSL Shell. Both of them are based on Gauss-Kronrod integration rules. The first method is non-adaptive and is called QNG while the seconde one, QAG, is adaptive. The adaptive method QAG is suitable as a general-purpose integrator, whereas the QNG method should be used only in particular cases where the function has a simple known smooth behavior.

Introduction

Each algorithm computes an approximation to a definite integral of the form,

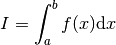
The user provides absolute and relative error bounds (epsabs, epsrel) which specify the following accuracy requirement,

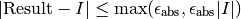
where Result is the numerical approximation obtained by the algorithm. The algorithm attempts to estimate the absolute error AbsErr = | Result - I | in such a way that the following inequality holds,

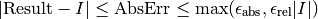
In short, the routines return the first approximation which has an absolute error smaller than epsabs or a relative error smaller than epsrel.

Note that this is an either-or constraint, not simultaneous. To compute to a specified absolute error, set epsrel to zero. To compute to a specified relative error, set epsabs to zero. The routines will fail to converge if the error bounds are too stringent, but always return the best approximation obtained up to that stage.

Functions

num.integ(f, a, b, epsabs, epsrel)

Compute the definite integral of the function f in the interval specified by a and b within the requested precision given by epsabs and epsrel. This function always use the adaptive QAG algorithm internally.

num.quad_prepare(spec)

Returns a function that can perform a numeric integration based on the options spec. The argument spec is used to choose the quadrature algorithm, the order and the limits for the adaptive search if applicable. The fields of spec that you should give are:

method

The quadrature algorithm. Available algorithms are qng and qag, the default is qag.

order

The order of the integration rule. The default value is 21.

limits

The maximum number of subdivisions for adaptive algorithms. The default value is 64.

Usage Example

Here a simple example that shows how to plot the Bessel function using its integral definition:

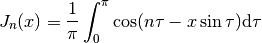
The function num.quad_prepare() is used to prepare the quadrature function. The function returned is then called many times to obtain :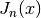

use 'math'

epsabs, epsrel = 1e-6, 0.01

function bessel_gen(n, q)
   local xs
   local fint = function(t) return cos(n*t - xs*sin(t)) end
   return function(x)
             xs = x
             return q(fint, 0, pi, epsabs, epsrel) / pi
          end
end

-- we get the 'qag' integration rule with default options
q = num.quad_prepare {method= 'qag'}

J7 = bessel_gen(7, q)

graph.fxplot(J7, 0, 50)