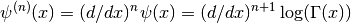Special functions¶
GSL Shell has moved
The project, its documentation and the release packages are now hosted on Github. Please find here the user manual.
The library includes routines for calculating the values of Airy functions, Bessel functions, Clausen functions, Coulomb wave functions, Coupling coefficients, the Dawson function, Debye functions, Dilogarithms, Elliptic integrals, Jacobi elliptic functions, Error functions, Exponential integrals, Fermi-Dirac functions, Gamma functions, Gegenbauer functions, Hypergeometric functions, Laguerre functions, Legendre functions and Spherical Harmonics, the Psi (Digamma) Function, Synchrotron functions, Transport functions, Trigonometric functions and Zeta functions. Any error returned by the special function (such as invalid input domains, etc...) will be signaled.
Overview¶
Airy Functions¶
- sf.airyAi(x)¶
- sf.airyBi(x)¶
The Airy functions
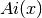 and
and 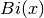 are defined by the integral representations,
are defined by the integral representations,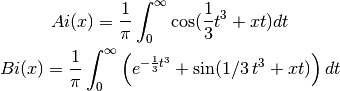
For further information see Abramowitz & Stegun, Section 10.4.
- sf.airyAi_scaled(x)¶
- sf.airyBi_scaled(x)¶
These routines compute a scaled version of the Airy function
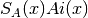 .
For x>0 the scaling factor
.
For x>0 the scaling factor 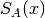 is
is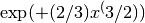
and is 1 for x<0.
- sf.airyAi_deriv(x)¶
- sf.airyAi_deriv_scaled(x)¶
- sf.airyBi_deriv(x)¶
- sf.airyBi_deriv_scaled(x)¶
These routines compute the Airy function derivatives and their scaled version with the same scaling factor as the airyAi_scaled and airyBi_scaled versions.
- sf.airyAi_zero(n)¶
- sf.airyAi_deriv_zero(n)¶
- sf.airyBi_zero(n)¶
- sf.airyBi_deriv_zero(n)¶
Return the n-th zero of the respective functions or their derivatives.
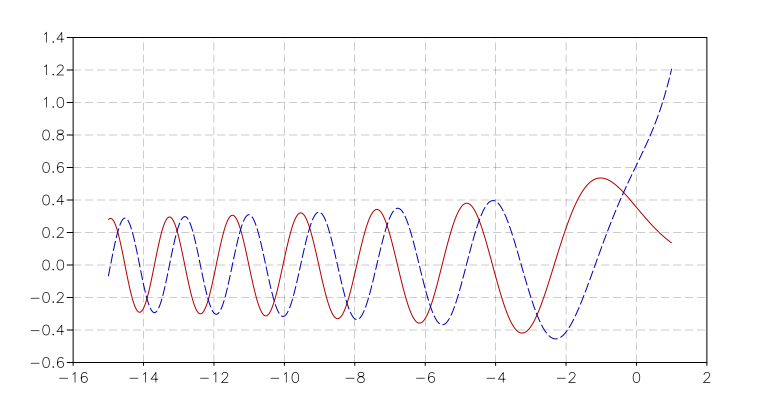
Airy functions Ai and Bi.
Bessel Functions¶
- sf.besselJ(n, x)¶
These routines compute the regular cylindrical Bessel function of n-th order, Jn(x)
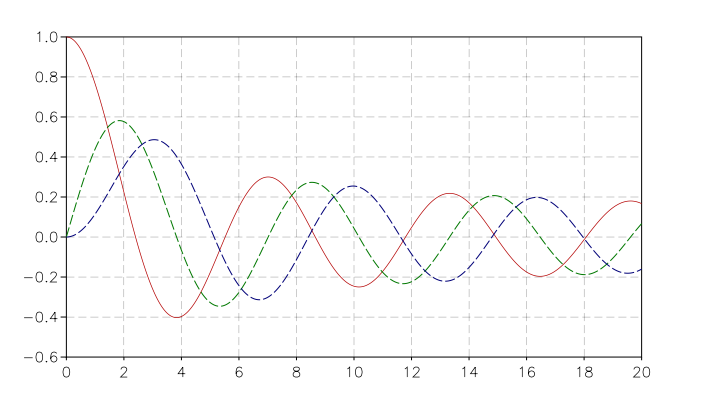
Bessel functions J0(red), J1(green), J2(blue)
- sf.besselJ_zero(n, s)¶
Return the s-th zero of the Bessel Jn function.
- sf.besselY(n, x)¶
These routines compute the irregular cylindrical Bessel function of n-th order, Yn(x)
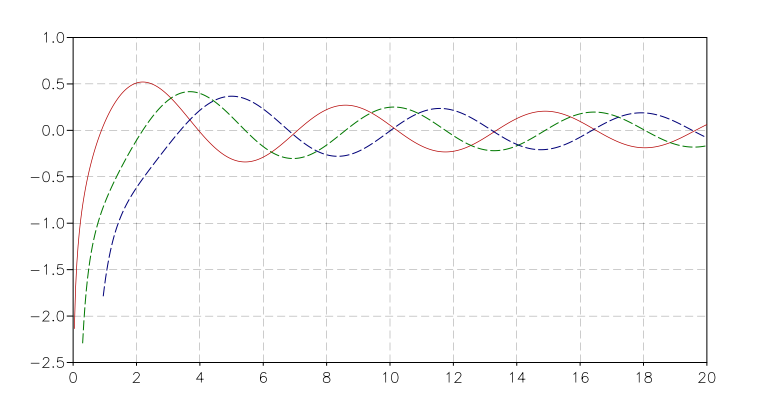
Bessel functions Y0(red), Y1(green), Y2(blue)
- sf.besselYnu(nu, x)¶
Compute the irregular cylindrical Bessel function of fractional order
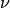 ,
, 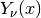 .
.
- sf.besselI(n, x)¶
- sf.besselI_scaled(n, x)¶
Regular modified cylindrical Bessel function of n-th order and their scaled version.
- sf.besselInu(n, x)¶
- sf.besselInu_scaled(n, x)¶
These routines compute the (scaled) regular modified Bessel function of fractional order
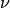 with
with 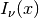 for x>0, nu>0.
for x>0, nu>0.
- sf.besselK(n, x)¶
- sf.besselK_scaled(n, x)¶
Irregular modified cylindrical Bessel function of order n and their scaled version.
- sf.besselKnu(nu, x)¶
- sf.bessellnKnu(nu, x)¶
- sf.besselKnu_scaled(nu, x)¶
Compute the (scaled or logarithm) irregular modified Bessel function of fractional order
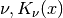 for x>0, nu>0.
for x>0, nu>0.
- sf.besselj(l, x)¶
Compute the regular spherical Bessel function of l-th order.
- sf.bessely(l, x)¶
Compute the irregular spherical Bessel function of l-th order.
- sf.besseli_scaled(l, x)¶
Compute the scaled regular modified spherical Bessel function of l-th order.
- sf.besselk(l, x)¶
Compute the irregular modified spherical Bessel function of l-th order.
Clausen Function¶
- sf.clausen(x)¶
The Clausen function is defined by the following integral,
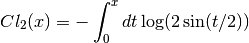
It is related to the dilogarithm by
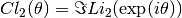 .
.
Coulomb Functions¶
- sf.hydrogenicR_1(Z, r)¶
These routines compute the lowest-order normalized hydrogenic bound state radial wavefunction
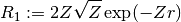
- sf.hydrogenicR(n, l, Z, r)¶
These routines compute the n-th normalized hydrogenic bound state radial wave function,
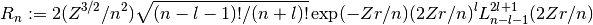
where
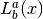 is the generalized Laguerre polynomial (see Laguerre Functions).
The normalization is chosen such that the wave function
is the generalized Laguerre polynomial (see Laguerre Functions).
The normalization is chosen such that the wave function 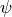 is given by
is given by 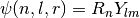 .
.
- sf.coulomb_wave_FG(eta, x, L_F, k)¶
This function computes the Coulomb wave functions
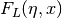 ,
, 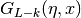 and their derivatives
and their derivatives 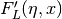 ,
, 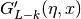 with respect to x.
The parameters are restricted to L, L-k > -1/2, x > 0 and integer k.
with respect to x.
The parameters are restricted to L, L-k > -1/2, x > 0 and integer k.Note that L itself is not restricted to being an integer. The results are returned as:
F, Fp, G, Gp, exp_F, exp_G = coulomb_wave_FG(eta, x, L_F,k)
with Fp and Gp being the derivates. If an overflow occurs, GSL_EOVRFLW is returned as an error and scaling exponents are stored in the return values exp_F, exp_G.
- sf.coulomb_CL(L, eta)¶
This function computes the Coulomb wave function normalization constant
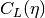 for L > -1.
for L > -1.
Coupling Coefficients¶
- sf.coupling_3j(two_ja, two_jb, two_jc, two_ma, two_mb, two_mc)¶
These routines compute the Wigner 3-j coefficient,
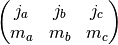
where the arguments are given in half-integer units, ja = two_ja/2, ma = two_ma/2, etc.
- sf.coupling_6j(two_ja, two_jb, two_jc, two_ma, two_mb, two_mc)¶
These routines compute the Wigner 6-j coefficient,
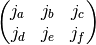
where the arguments are given in half-integer units, ja = two_ja/2, ma = two_ma/2, etc.
- sf.coupling_9j(two_ja, two_jb, two_jc, two_jd, two_je, two_jf, two_jg, two_jh, two_ji)¶
These routines compute the Wigner 9-j coefficient,
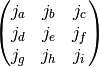
where the arguments are given in half-integer units, ja = two_ja/2, ma = two_ma/2, etc.
Dawson Function¶
- sf.dawson(x)¶
The Dawson integral is defined by
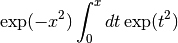
A table of Dawson’s integral can be found in Abramowitz & Stegun, Table 7.5.
Debye Functions¶
- sf.debye(n, x)¶
The Debye functions
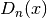 are defined by the following integral,
are defined by the following integral,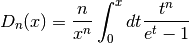
For further information see Abramowitz & Stegun, Section 27.1.
Dilogarithms¶
- sf.dilog(x)¶
These routines compute the dilogarithm for a real argument. In Lewin’s notation this is Li2(x), the real part of the dilogarithm of a real x. It is defined by the integral representation
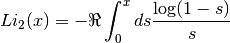
Note that
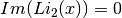 for x <= 1, and
for x <= 1, and 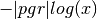 for x > 1.
for x > 1.Note that Abramowitz & Stegun refer to the Spence integral
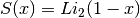 as the dilogarithm rather than
as the dilogarithm rather than 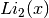 .
.
- sf.cdilog(z)¶
Compute the dilogarithm for a complex argument.
Elliptic Integrals¶
The Legendre forms of elliptic integrals 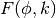 ,
, 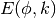 and
and 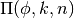 are defined by,
are defined by,
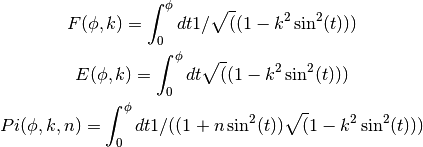
The complete Legendre forms are denoted by 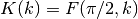 and
and 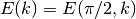 .
The notation used here is based on Carlson, Numerische Mathematik 33 (1979) 1 and differs slightly from that used by Abramowitz & Stegun, where the functions are given in terms of the parameter
.
The notation used here is based on Carlson, Numerische Mathematik 33 (1979) 1 and differs slightly from that used by Abramowitz & Stegun, where the functions are given in terms of the parameter 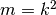 and n is replaced by -n.
and n is replaced by -n.
The Carlson symmetric forms of elliptical integrals 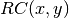 ,
, 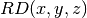 ,
, 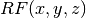 and
and 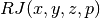 are defined by,
are defined by,
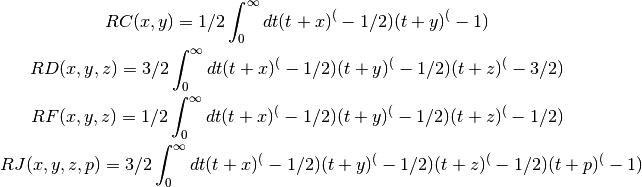
- sf.ellint_D(phi, k, n)¶
These functions compute the incomplete elliptic integral
 which is defined through the Carlson form
which is defined through the Carlson form 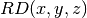 by the following relation,
by the following relation,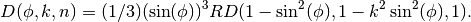
The argument n is not used and will be removed in a future release.
- sf.ellint_E(phi, lk)¶
These routines compute the incomplete elliptic integral
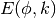 to the accuracy specified by the mode variable mode. Note that Abramowitz & Stegun define this function in terms of the parameter
to the accuracy specified by the mode variable mode. Note that Abramowitz & Stegun define this function in terms of the parameter 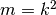 .
.
- sf.ellint_F(phi, k)¶
These routines compute the incomplete elliptic integral
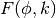 to the accuracy specified by the mode variable mode. Note that Abramowitz & Stegun define this function in terms of the parameter
to the accuracy specified by the mode variable mode. Note that Abramowitz & Stegun define this function in terms of the parameter 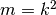 .
.
- sf.ellint_P(phi, k, n)¶
These routines compute the incomplete elliptic integral
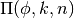 to the accuracy specified by the mode variable mode. Note that Abramowitz & Stegun define this function in terms of the parameters
to the accuracy specified by the mode variable mode. Note that Abramowitz & Stegun define this function in terms of the parameters 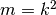 and
and 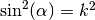 , with the change of sign
, with the change of sign 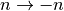 .
.
- sf.ellint_RC(x, y)¶
These routines compute the incomplete elliptic integral
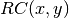 to the accuracy specified by the mode variable mode.
to the accuracy specified by the mode variable mode.
- sf.ellint_RD(x, y, z)¶
These routines compute the incomplete elliptic integral
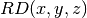 to the accuracy specified by the mode variable mode.
to the accuracy specified by the mode variable mode.
- sf.ellint_RF(x, y, z)¶
These routines compute the incomplete elliptic integral
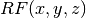 to the accuracy specified by the mode variable mode.
to the accuracy specified by the mode variable mode.
- sf.ellint_RJ(x, y, z, p)¶
These routines compute the incomplete elliptic integral
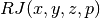 to the accuracy specified by the mode variable mode.
to the accuracy specified by the mode variable mode.
Elliptic Function¶
- sf.elljac(u, m)¶
This function computes the Jacobian elliptic functions
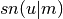 ,
, 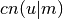 ,
, 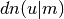 by descending Landen transformations.
It returns sn, cn and dn as:
by descending Landen transformations.
It returns sn, cn and dn as:sn, cn, dn = elljac(u, m)
Error Functions¶
- sf.erf(x)¶
The error function erf(x)
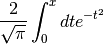
- sf.erfc(x)¶
- sf.log_erfc(x)¶
These routines compute the (logarithmic) complementary error function
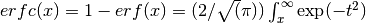 .
.
- sf.erf_Q(1)¶
These routines compute the upper tail of the Gaussian probability function
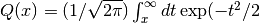
- sf.erf_Z(1)¶
These routines compute the Gaussian probability density function
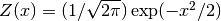 .
.
- sf.hazard(x)¶
These routines compute the hazard function for the normal distribution.
Exponential Functions¶
- sf.exp(x)¶
These routines provide an exponential function
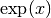 .
.
- sf.exp_err(x, dx)¶
This function exponentiates x with an associated absolute error dx.
- sf.exp_mult(x, y)¶
These routines exponentiate x and multiply by the factor y to return the product
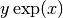 .
.
- sf.exp_mult_err(x, dx, y, dy)¶
This routine computes the product
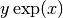 for the quantities x, y with associated absolute errors dx, dy.
for the quantities x, y with associated absolute errors dx, dy.
- sf.expm1(x)¶
These routines compute the quantity
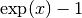 using an algorithm that is accurate for small x.
using an algorithm that is accurate for small x.
- sf.exprel(x)¶
These routines compute the quantity
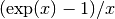 using an algorithm that is accurate for small x. For small x the algorithm is based on the expansion
using an algorithm that is accurate for small x. For small x the algorithm is based on the expansion 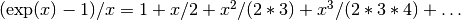 .
.
- sf.exprel_2(x)¶
These routines compute the quantity
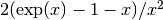 using an algorithm that is accurate for small x. For small x the algorithm is based on the expansion
using an algorithm that is accurate for small x. For small x the algorithm is based on the expansion 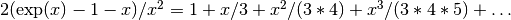 .
.
- sf.exprel_n(n, 1)¶
These routines compute the N-relative exponential given by,
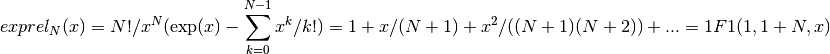
Exponential Integrals¶
- sf.expint_E(n, x)¶
These routines compute the exponential integral
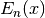 of order n,
of order n,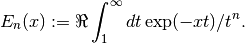
- sf.expint_Ei(x)¶
These routines compute the exponential integral
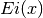 ,
,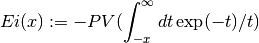
where PV denotes the principal value of the integral.
- sf.Shi(x)¶
These routines compute the integral
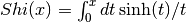 .
.
- sf.Chi(x)¶
These routines compute the integral
![Chi(x) := \Re[ \gamma_E + \log(x) + \int_0^x dt (\cosh(t)-1)/t]](_images/math/94ceae8be1a2ff4932a44d5d2d08c14ed7bbc1bf.png) , where
, where 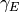 is the Euler constant (available as the macro M_EULER).
is the Euler constant (available as the macro M_EULER).
- sf.expint_3(x)¶
These routines compute the third-order exponential integral
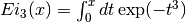 for x >= 0.
for x >= 0.
- sf.Si(x)¶
These routines compute the Sine integral
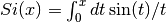 .
.
- sf.Ci(x)¶
These routines compute the Cosine integral
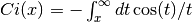 for x > 0.
for x > 0.
- sf.atanint(x)¶
These routines compute the Arctangent integral, which is defined as
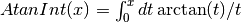 .
.
Fermi Dirac Function¶
- sf.fermi_dirac(n, x)¶
The complete Fermi-Dirac integral Fn(x) is given by,
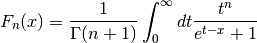
Note that the Fermi-Dirac integral is sometimes defined without the normalization factor in other texts.
- sf.fermi_dirac_inc(x, b)¶
These routines compute the incomplete Fermi-Dirac integral with an index of zero,
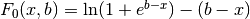 .
.The incomplete Fermi-Dirac integral
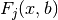 is given by,
is given by,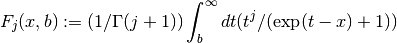
Gamma and Beta Functions¶
- sf.Shi(x)
Compute the integral
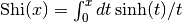 .
.
- sf.Chi(x)
Compute the integral
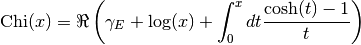
where γE is the Euler constant.
- sf.Si(x)
Compute the Sine integral
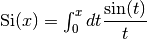 .
.
- sf.Ci(x)
Compute the Cosine integral
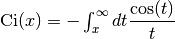 for x > 0.
for x > 0.
- sf.atanint(x)
compute the Arctangent integral, which is defined as
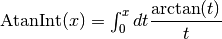 .
.
- sf.fact(n)¶
Compute the factorial n!. The factorial is related to the Gamma function by
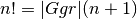 .
.
- sf.doublefact(n)¶
Compute the double factorial
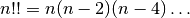 .
.
- sf.lnfact(n)¶
These routines compute the logarithm of the factorial of N, log(n!). The algorithm is faster than computing ln(Γ (n+1)).
- sf.lndoublefact(n)¶
Compute the logarithm of the double factorial of N, log(n!!).
- sf.choose(n, k)¶
Compute the combinatorial factor
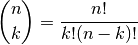
- sf.lnchoose(n, k)¶
Compute the logarithm of “n choose m”. This is equivalent to the sum
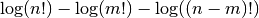 .
.
- sf.gamma(x)¶
Compute the Gamma function Γ (x), subject to x not being a negative integer or zero. The function is computed using the real Lanczos method.
- sf.lngamma(x)¶
Compute the logarithm of the Gamma function,
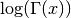 , subject to x not being a negative integer or zero. For x<0 the real part of
, subject to x not being a negative integer or zero. For x<0 the real part of 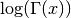 is returned, which is equivalent to
is returned, which is equivalent to 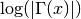 . The function is computed using the real Lanczos method.
. The function is computed using the real Lanczos method.
- sf.gammastar(x)¶
These routines compute the regulated Gamma Function
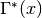 for x > 0. The regulated gamma function is given by,
for x > 0. The regulated gamma function is given by,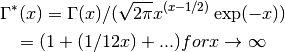
and is a useful suggestion of Temme.
- sf.gammainv(x)¶
These routines compute the reciprocal of the gamma function,
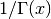 using the real Lanczos method.
using the real Lanczos method.
- sf.lngammac(z)¶
This routine computes
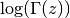 for complex z and z not a negative integer or zero, using the complex Lanczos method.
The returned parameters are
for complex z and z not a negative integer or zero, using the complex Lanczos method.
The returned parameters are 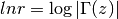 and
and ![arg = \arg(\Gamma(z)) in (-\pi,\pi]](_images/math/c66a65f7926a081460fc775a9729968a2f6f5a5d.png) .
Note that the phase part (arg) is not well-determined when
.
Note that the phase part (arg) is not well-determined when 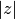 is very large, due to inevitable roundoff in restricting to (-pi,pi]. This will result in a GSL_ELOSS error when it occurs. The absolute value part (lnr), however, never suffers from loss of precision.
is very large, due to inevitable roundoff in restricting to (-pi,pi]. This will result in a GSL_ELOSS error when it occurs. The absolute value part (lnr), however, never suffers from loss of precision.The functions returns:
lnr, arg = lngammac(z)
- sf.beta(a, b)¶
These routines compute the Beta Function,
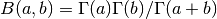 subject to a and b not being negative integers.
subject to a and b not being negative integers.
- sf.lnbeta(a, b)¶
These routines compute the logarithm of the Beta Function,
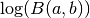 subject to a and b not being negative integers.
subject to a and b not being negative integers.
- sf.beta_inc(a, b, x)¶
These routines compute the normalized incomplete Beta function
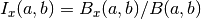 where
where 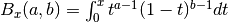 for 0 <= x <= 1.
For a > 0, b > 0 the value is computed using a continued fraction expansion. For all other values it is computed using the relation
for 0 <= x <= 1.
For a > 0, b > 0 the value is computed using a continued fraction expansion. For all other values it is computed using the relation 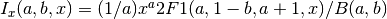 .
.
- sf.taylorcoeff(n, x)¶
These routines compute the Taylor coefficient
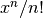 for x >= 0, n >= 0.
for x >= 0, n >= 0.
- sf.poch(a, x)¶
These routines compute the Pochhammer symbol
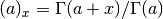 . The Pochhammer symbol is also known as the Apell symbol and sometimes written as (a,x). When a and a+x are negative integers or zero, the limiting value of the ratio is returned.
. The Pochhammer symbol is also known as the Apell symbol and sometimes written as (a,x). When a and a+x are negative integers or zero, the limiting value of the ratio is returned.
- sf.lnpoch(a, x)¶
These routines compute the logarithm of the Pochhammer symbol,
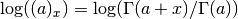 .
.
- sf.pochrel(a, x)¶
These routines compute the relative Pochhammer symbol
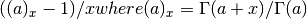 .
.
- sf.gamma_inc(a, x)¶
These functions compute the unnormalized incomplete Gamma Function
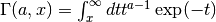 for a real and x >= 0.
for a real and x >= 0.
- sf.gamma_inc_Q(a, x)¶
These routines compute the normalized incomplete Gamma Function
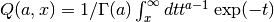 for a > 0, x >= 0.
for a > 0, x >= 0.
- sf.gamma_inc_P(a, x)¶
These routines compute the complementary normalized incomplete Gamma Function
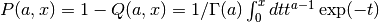 for a > 0, x >= 0. Note that Abramowitz & Stegun call P(a,x) the incomplete gamma function (section 6.5).
for a > 0, x >= 0. Note that Abramowitz & Stegun call P(a,x) the incomplete gamma function (section 6.5).
Gegenbauer Functions¶
- sf.gegenpoly(n, lambda, x)¶
These functions evaluate the Gegenbauer polynomial
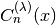 for a specific value of n, lambda, x subject to
for a specific value of n, lambda, x subject to 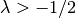 , n >= 0.
, n >= 0.
Hypergeometric functions¶
- sf.hyperg0F1(a, b)¶
These routines compute the hypergeometric function
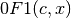 .
.
- sf.hyperg1F1(m, n, x)¶
These routines compute the confluent hypergeometric function
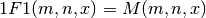 . The parameters m and n can be integer or real numbers.
. The parameters m and n can be integer or real numbers.
- sf.hypergU(m, n, x)¶
These routines compute the confluent hypergeometric function
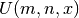 . The parameters m and n can be integer or real numbers.
. The parameters m and n can be integer or real numbers.
- sf.hyperg2F1(a, b, c, x)¶
These routines compute the Gauss hypergeometric function
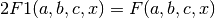 for
for 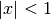 .
.If the arguments (a,b,c,x) are too close to a singularity then the function can return the error code GSL_EMAXITER when the series approximation converges too slowly. This occurs in the region of x=1, c - a - b = m for integer m.
- sf.hyperg2F1conj(a, c, x)¶
These routines compute the Gauss hypergeometric function
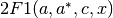 where a is complex parameter, c and x are real parameters with
where a is complex parameter, c and x are real parameters with 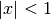 .
.
Laguerre Functions¶
- sf.laguerre(n, a, x)¶
The generalized Laguerre polynomials are defined in terms of confluent hypergeometric functions as
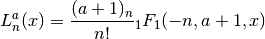
and are sometimes referred to as the associated Laguerre polynomials. They are related to the plain Laguerre polynomials
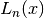 by
by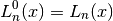
and
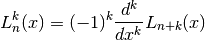
For more information see Abramowitz & Stegun, Chapter 22.
Lambert W Functions¶
Lambert’s W functions, W(x), are defined to be solutions of the equation 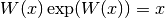 .
This function has multiple branches for x < 0; however, it has only two real-valued branches.
We define
.
This function has multiple branches for x < 0; however, it has only two real-valued branches.
We define 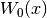 to be the principal branch, where W > -1 for x < 0, and
to be the principal branch, where W > -1 for x < 0, and 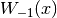 to be the other real branch, where W < -1 for x < 0.
to be the other real branch, where W < -1 for x < 0.
- sf.lambertW0(x)¶
These compute the principal branch of the Lambert W function,
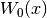 .
.
- sf.lambertWm1(x)¶
These compute the secondary real-valued branch of the Lambert W function,
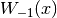 .
.
Legendre Functions and Spherical Harmonics¶
- sf.legendreP(n, x)¶
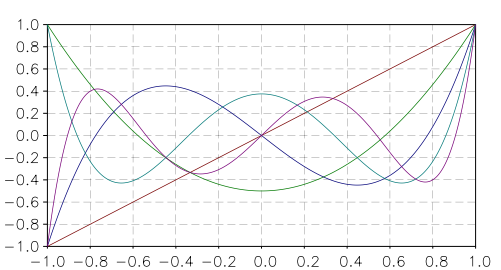
Legendre polynomials
These functions evaluate the Legendre polynomial
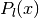 for a specific value of l, x subject to l >= 0,
for a specific value of l, x subject to l >= 0, 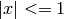
- sf.legendreQ(n, x)¶
These routines compute the Legendre function
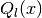 for x > -1, x != 1 and l >= 0.
for x > -1, x != 1 and l >= 0.
- sf.legendrePlm(l, m, x)¶
These routines compute the associated Legendre polynomial
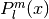 for m >= 0, l >= m,
for m >= 0, l >= m, 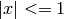 .
.
- sf.legendresphPlm(l, m, x)¶
These routines compute the normalized associated Legendre polynomial
 suitable for use in spherical harmonics. The parameters must satisfy m >= 0, l >= m,
suitable for use in spherical harmonics. The parameters must satisfy m >= 0, l >= m, 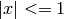 . Theses routines avoid the overflows that occur for the standard normalization of
. Theses routines avoid the overflows that occur for the standard normalization of 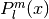 .
.
- sf.conicalP(n, lambda, x)¶
These routines compute the regular Spherical Conical Function
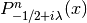 for x > -1 where n in {-12, 0, 12, 1}
for x > -1 where n in {-12, 0, 12, 1}
- sf.conicalPsphreg(l, lambda, x)¶
These routines compute the Regular Spherical Conical Function
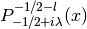 for x > -1, l >= -1.
for x > -1, l >= -1.
- sf.conicalPcylreg(m, lambda, x)¶
These routines compute the Regular Cylindrical Conical Function
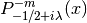 for x > -1, m >= -1.
for x > -1, m >= -1.
- sf.legendre_H3d(l, lambda, eta)¶
These routines compute the l-th radial eigenfunction of the Laplacian on the 3-dimensional hyperbolic space
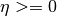 , l >= 0. In the flat limit this takes the form
, l >= 0. In the flat limit this takes the form 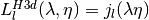 .
.
Psi (Digamma) Functions¶
The polygamma functions of order n are defined by
where 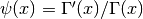 is known as the digamma function.
is known as the digamma function.
- sf.psi(x)¶
These routines compute the digamma function
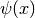 for general x, x ne 0.
for general x, x ne 0.
- sf.psi_1(x)¶
These routines compute the Trigamma function
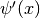 for general x.
for general x.
- sf.1piy(y)¶
These routines compute the real part of the digamma function on the line 1+i y,
![\Re[\psi(1 + i y)]](_images/math/761307a0ce27e7207ff995740768a98b3ff9a6f8.png) .
.
- sf.psi_n(n, x)¶
These routines compute the polygamma function
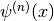 for n >= 0, x > 0.
for n >= 0, x > 0.
Synchrotron Functions¶
- sf.synchrotron1(n, x)¶
These routines compute the first synchrotron function
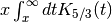 for x >= 0.
for x >= 0.
- sf.synchrotron2(n, x)¶
These routines compute the second synchrotron function
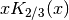 for x >= 0.
for x >= 0.
Transport Functions¶
The transport functions J(n,x) are defined by the integral representations 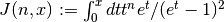 .
.
- sf.transport(n, x)¶
These routines compute the transport function
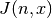 with
with 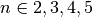
Zeta Functions¶
- sf.zeta(s)¶
The Riemann zeta function is defined by the infinite sum
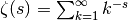 .
These routines compute the Riemann zeta function
.
These routines compute the Riemann zeta function 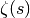 for arbitrary s,
for arbitrary s, 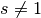 .
.
- sf.zetam1(s)¶
For large positive argument, the Riemann zeta function approaches one. In this region the fractional part is interesting, and therefore we need a function to evaluate it explicitly. These routines compute
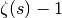 for arbitrary s,
for arbitrary s, 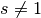 .
.
- sf.eta(s)¶
The eta function is defined by
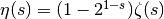 .
These routines compute the eta function eta(s) for arbitrary s.
.
These routines compute the eta function eta(s) for arbitrary s.
- sf.hzeta(s, q)¶
These routines compute the Hurwitz zeta function
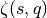 for s > 1, q > 0.
for s > 1, q > 0.
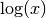 , for x > 0.
, for x > 0.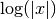 , for x ne 0.
, for x ne 0.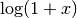 for x > -1 using an algorithm that is accurate for small x.
for x > -1 using an algorithm that is accurate for small x.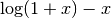 for x > -1 using an algorithm that is accurate for small x.
for x > -1 using an algorithm that is accurate for small x.