 |

|
Funciones | |
| int | pds_symetric_ber_bsc_model (double rho, unsigned int M, double *BER) |
Retorna la taza de erro de bit, 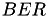 , en el problema CEO binario simétrico de M fontes , en el problema CEO binario simétrico de M fontes 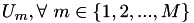 , donde , donde 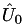 representa la mejor aproximación de representa la mejor aproximación de 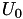 conociendo conociendo 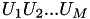 . Más... . Más... | |
| int | pds_vector_symetric_ber_bsc_model (const PdsVector *RHO, PdsRaNatural M, PdsVector *BER) |
Retorna un vector con las tazas de erro de bit, 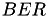 , (para cada valor de probabilidad de error dentro del vector RHO) en el problema CEO binario simétrico de M fontes , (para cada valor de probabilidad de error dentro del vector RHO) en el problema CEO binario simétrico de M fontes 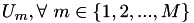 , donde , donde 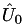 representa la mejor aproximación de representa la mejor aproximación de 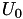 conociendo conociendo 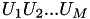 . Más... . Más... | |
| int | pds_joint_probability_bsc_model (PdsBVector *OmegaM, const PdsVector *Ps, double p0, double *JointProb) |
Encuentra la probabilidad conjunta 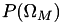 de tener en la salida de un grupo de canales BSC un conjunto de valores binarios formando un vector de tener en la salida de un grupo de canales BSC un conjunto de valores binarios formando un vector 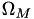 [5] . Más... [5] . Más... | |
| int | pds_joint_entropy_bsc_model (const PdsVector *Ps, double p0, double *HJoint) |
Encuentra la entropia conjunta 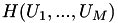 para M fontes generadas pasando una fuente U0, con probabilidade Pr(U0=1)=p0, atraves de M canales BSC con probabilidades de error Ps=[Ps0, Ps1, ..., Ps(M-1)] [5] . Más... para M fontes generadas pasando una fuente U0, con probabilidade Pr(U0=1)=p0, atraves de M canales BSC con probabilidades de error Ps=[Ps0, Ps1, ..., Ps(M-1)] [5] . Más... | |
| int | pds_probability_u0_omega_bsc_model (PdsBVector *OmegaM, const PdsVector *Ps, PdsBaBit U0, double p0, double *PcU0OmegaM, double *PjU0OmegaM) |
Encuentra las probabilidades condicionada 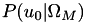 y conjunta y conjunta 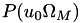 [5] . Más... [5] . Más... | |
| int | pds_entropy_u0_omega_bsc_model (const PdsVector *Ps, double p0, double *HCond) |
Encuentra la entropia condicionada. 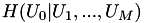 [5] . Más... [5] . Más... | |
| int | pds_symetric_entropy_u0_omega_bsc_model (double rho, PdsBaNatural M, double *HCond) |
Encuentra la entropia condicionada HCond [4] . 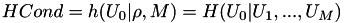 . Este es el caso cuando todas las probabilidades de error son iguales a rho. . Este es el caso cuando todas las probabilidades de error son iguales a rho. 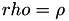 . Más... . Más... | |
| int | pds_vector_symetric_entropy_u0_omega_bsc_model (PdsVector *RHO, PdsBaNatural M, PdsVector *HCOND) |
Encuentra la entropia condicionada HCond [4] . 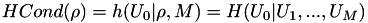 . Este es el caso cuando todas las probabilidades de error son iguales a rho. . Este es el caso cuando todas las probabilidades de error son iguales a rho. 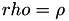 . Más... . Más... | |
| int | pds_symetric_joint_entropy_bsc_model (double rho, PdsRaNatural M, double *HJoint) |
Encuentra la entropia conjunta HJoint, 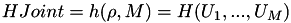 , de las señales a la salida de un bloque de de M fuentes binarias correlacionadas [2]. Más... , de las señales a la salida de un bloque de de M fuentes binarias correlacionadas [2]. Más... | |
| int | pds_inv_symetric_entropy_u0_omega_bsc_model (double HCond, short int M, double *rho) |
Encuentra la inversa 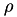 de la entropia condicionada HCond [4] . de la entropia condicionada HCond [4] . 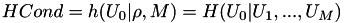 . Más... . Más... | |
| int | pds_inv_symetric_joint_entropy_bsc_model (double HJoint, short int M, double *rho) |
Encuentra la inversa 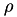 de la entropia conjunta de la entropia conjunta 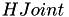 [2] . [2] . 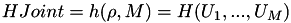 . Más... . Más... | |
| int pds_symetric_ber_bsc_model | ( | double | rho, |
| unsigned int | M, | ||
| double * | BER | ||
| ) |
Retorna la taza de erro de bit, 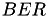 , en el problema CEO binario simétrico de M fontes
, en el problema CEO binario simétrico de M fontes 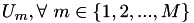 , donde
, donde 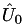 representa la mejor aproximación de
representa la mejor aproximación de 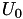 conociendo
conociendo 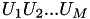 .
.
Estas fuentes son generadas pasando una fuente 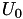 , con probabilidade
, con probabilidade 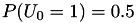 , atraves de M canales BSC con probabilidades de error
, atraves de M canales BSC con probabilidades de error 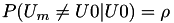 .
.

Quando M es impar :
![\[ BER= \sum_{j=(M+1)/2}^{M} {{M}\choose{j}} {\rho}^j (1-\rho)^{M-j} \]](form_7.png)
Quando M es par :
![\[ BER= \sum_{j=(M/2)+1}^{M} {{M}\choose{j}} {\rho}^j (1-\rho)^{M-j}+0.5 {{M}\choose{M/2}} {\rho}^{M/2} (1-\rho)^{M/2} \]](form_8.png)
!!!!CUIDADO ACTUAL 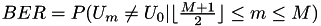 !!!!!
!!!!!
The formula for calculus of BER is in [3] and other simplification in [1] [2] .
| [in] | rho | Es la probabilidad de error de los canales BSC. 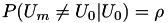 . . |
| [in] | M | Es el número de canales BSC. |
| [out] | BER | es la taza de error de bit. |
| int pds_vector_symetric_ber_bsc_model | ( | const PdsVector * | RHO, |
| PdsRaNatural | M, | ||
| PdsVector * | BER | ||
| ) |
Retorna un vector con las tazas de erro de bit, 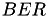 , (para cada valor de probabilidad de error dentro del vector RHO) en el problema CEO binario simétrico de M fontes
, (para cada valor de probabilidad de error dentro del vector RHO) en el problema CEO binario simétrico de M fontes 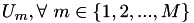 , donde
, donde 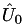 representa la mejor aproximación de
representa la mejor aproximación de 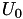 conociendo
conociendo 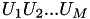 .
.
Estas fuentes son generadas pasando una fuente 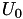 , con probabilidade
, con probabilidade 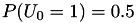 , atraves de M canales BSC con probabilidades de error
, atraves de M canales BSC con probabilidades de error 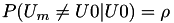 .
.

Quando M es impar :
![\[ BER= \sum_{j=(M+1)/2}^{M} {{M}\choose{j}} {\rho}^j (1-\rho)^{M-j} \]](form_7.png)
Quando M es par :
![\[ BER= \sum_{j=(M/2)+1}^{M} {{M}\choose{j}} {\rho}^j (1-\rho)^{M-j}+0.5 {{M}\choose{M/2}} {\rho}^{M/2} (1-\rho)^{M/2} \]](form_8.png)
!!!!CUIDADO ACTUAL 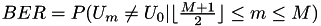 !!!!!
!!!!!
The formula for calculus of BER is in [3] and other simplification in [1] [2] .
| [in] | RHO | Es un vector con las probabilidades de error 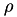 a ser evaluadas. a ser evaluadas. 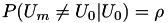 . . |
| [in] | M | Es el número de canales BSC. |
| [out] | BER | Es un vector con la taza de error de bit para cada valor de probabilidades de error 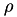 en el vector RHO. en el vector RHO. |
| int pds_joint_probability_bsc_model | ( | PdsBVector * | OmegaM, |
| const PdsVector * | Ps, | ||
| double | p0, | ||
| double * | JointProb | ||
| ) |
Encuentra la probabilidad conjunta 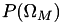 de tener en la salida de un grupo de canales BSC un conjunto de valores binarios formando un vector
de tener en la salida de un grupo de canales BSC un conjunto de valores binarios formando un vector 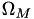 [5] .
[5] .

Conocido un conjunto 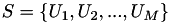 de fuentes binarias, estas son construidas pasando la fuente binaria
de fuentes binarias, estas son construidas pasando la fuente binaria 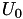 con
con 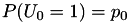 , por M canales BSC con probabilidad de error
, por M canales BSC con probabilidad de error 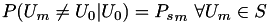 . Si definimos el vector
. Si definimos el vector 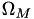 como:
como:
![\[ \Omega_M \equiv \{u_m: U_m=u_m \forall U_m \in S\} \]](form_17.png)
Entonces este tendrá como probabilidad:
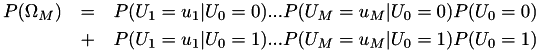
| [in] | OmegaM | Es un caso de ocurrencia del vector binario. |
| [in] | Ps | Es el vector de probabilidades de error de las fuentes BSC. Ps=[Ps0, Ps1, ..., Ps(M-1)]. 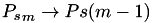 . . |
| [in] | p0 | Probabilida Pr(U0=1)=p0 de la fuente U0. |
| [out] | JointProb | probabilidad conjuta del caso de ocurrencia de OmegaM. |
| int pds_joint_entropy_bsc_model | ( | const PdsVector * | Ps, |
| double | p0, | ||
| double * | HJoint | ||
| ) |
Encuentra la entropia conjunta 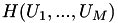 para M fontes generadas pasando una fuente U0, con probabilidade Pr(U0=1)=p0, atraves de M canales BSC con probabilidades de error Ps=[Ps0, Ps1, ..., Ps(M-1)] [5] .
para M fontes generadas pasando una fuente U0, con probabilidade Pr(U0=1)=p0, atraves de M canales BSC con probabilidades de error Ps=[Ps0, Ps1, ..., Ps(M-1)] [5] .

![\[ H(U_1, U_2, ..., U_M)= \sum_{U_1, U_2, ... U_M} P(U_1, U_2, ..., U_M)~log_2(P(U_1, U_2, ..., U_M)) \]](form_21.png)
![\[ P(U_m \neq U_0| U_0)={P_s}_{m} \]](form_22.png)
| [in] | Ps | Es el vector de probabilidades de error de las fuentes BSC. Ps=[Ps0, Ps1, ..., Ps(M-1)]. 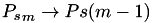 . . |
| [in] | p0 | Probabilida Pr(U0=1)=p0. |
| [out] | HJoint | Es el resultado, la entropia conjuta. |
| int pds_probability_u0_omega_bsc_model | ( | PdsBVector * | OmegaM, |
| const PdsVector * | Ps, | ||
| PdsBaBit | U0, | ||
| double | p0, | ||
| double * | PcU0OmegaM, | ||
| double * | PjU0OmegaM | ||
| ) |
Encuentra las probabilidades condicionada 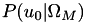 y conjunta
y conjunta 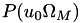 [5] .
[5] .

Conocido un conjunto 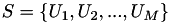 de fuentes binarias, estas son construidas pasando la fuente binaria
de fuentes binarias, estas son construidas pasando la fuente binaria 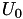 con
con 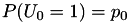 , por M canales BSC con probabilidad de error
, por M canales BSC con probabilidad de error 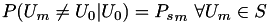 . Asi, definimos el vector
. Asi, definimos el vector 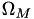 como:
como:
![\[ \Omega_M \equiv \{u_m: U_m=u_m \forall U_m \in S\} \]](form_17.png)
Entonces este tendrá como probabilidad:
![\[ P(u_0\Omega_M) = P(U_1=u_1|U_0=u_0) ... P(U_M=u_M|U_0=u_0) P(U_0=u_0) \]](form_25.png)
![\[ P(u_0|\Omega_M) = \frac{P(u_0\Omega_M) }{P(\Omega_M)} \]](form_26.png)
Sabiendo que:
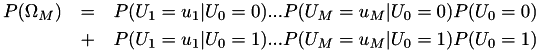
| [in] | OmegaM | Es un caso de ocurrencia del vector binario. |
| [in] | Ps | Es el vector de probabilidades de error de las fuentes BSC. Ps=[Ps0, Ps1, ..., Ps(M-1)]. 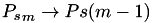 . . |
| [in] | U0 | Valor de U0 a analiza. |
| [in] | p0 | Probabilida Pr(U0=1)=p0 de la fuente U0. |
| [out] | PcU0OmegaM | Retorna la probabilidad condicionada. 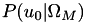 . . |
| [out] | PjU0OmegaM | Retorna la probabilidad conjuta. 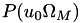 . . |
| int pds_entropy_u0_omega_bsc_model | ( | const PdsVector * | Ps, |
| double | p0, | ||
| double * | HCond | ||
| ) |
Encuentra la entropia condicionada. 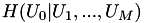 [5] .
[5] .

Dadas M fontes Um , m ={1,2,...,M}, generadas pasando una fuente U0, con probabilidade Pr(U0=1)=p0, atraves de M canales BSC con probabilidades de error Ps=[Ps0, Ps1, ..., Ps(M-1)].
![\[ H(U_0|U_1, U_2, ..., U_M)= \sum_{U_0,U_1, U_2, ... U_M} P(U_0,U_1, U_2, ..., U_M)~log_2(P(U_0|U_1, U_2, ..., U_M)) \]](form_28.png)
![\[ P(U_m \neq U_0| U_0)={P_s}_{m} \]](form_22.png)
| [in] | Ps | Es el vector de probabilidades de error de las fuentes BSC. Ps=[Ps0, Ps1, ..., Ps(M-1)]. 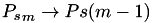 . . |
| [in] | p0 | Probabilida Pr(U0=1)=p0. |
| [out] | HCond | Entropia condicionada. 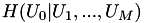 . . |
| int pds_symetric_entropy_u0_omega_bsc_model | ( | double | rho, |
| PdsBaNatural | M, | ||
| double * | HCond | ||
| ) |
Encuentra la entropia condicionada HCond [4] . 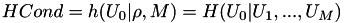 . Este es el caso cuando todas las probabilidades de error son iguales a rho.
. Este es el caso cuando todas las probabilidades de error son iguales a rho. 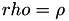 .
.

Dadas M fontes Um , m ={1,2,...,M}, generadas pasando una fuente U0, con probabilidade Pr(U0=1)=0.5, atraves de M canales BSC con probabilidades de error Ps=[rho, rho, ..., rho].
![\[ h(U_0| \rho,M)= \sum_{k=0}^{M} {M \choose k} \rho^k (1-\rho)^{M-k}~log_2 \left ( 1 + \{ \frac{\rho}{1-\rho} \}^{M-2 k} \right ) \]](form_31.png)
![\[ P(U_m \neq U_0| U_0)=\rho \]](form_32.png)
| [in] | rho | Es la probabilidad de error de los canales BSC. 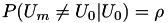 . . |
| [in] | M | Es el número de canales BSC. |
| [out] | HCond | Entropia condicionada. 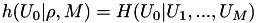 . . |
| int pds_vector_symetric_entropy_u0_omega_bsc_model | ( | PdsVector * | RHO, |
| PdsBaNatural | M, | ||
| PdsVector * | HCOND | ||
| ) |
Encuentra la entropia condicionada HCond [4] . 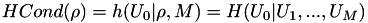 . Este es el caso cuando todas las probabilidades de error son iguales a rho.
. Este es el caso cuando todas las probabilidades de error son iguales a rho. 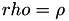 .
.
El vector HCOND 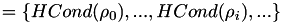 es cargado con los valores de entropia condicionada
es cargado con los valores de entropia condicionada 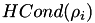 obtenidos por cada valor de de probabilidad de error
obtenidos por cada valor de de probabilidad de error 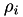 dentro del vector RHO.
dentro del vector RHO.

Dadas M fontes Um , m ={1,2,...,M}, generadas pasando una fuente U0, con probabilidade Pr(U0=1)=0.5, atraves de M canales BSC con probabilidades de error Ps=[rho, rho, ..., rho].
![\[ h(U_0| \rho,M)= \sum_{k=0}^{M} {M \choose k} \rho^k (1-\rho)^{M-k}~log_2 \left ( 1 + \{ \frac{\rho}{1-\rho} \}^{M-2 k} \right ) \]](form_31.png)
![\[ P(U_m \neq U_0| U_0)=\rho \]](form_32.png)
| [in] | RHO | Es un vecor con todas las probabilidades a evaluar como la probabilidad de error de todos los canales BSC. 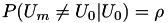 . . |
| [in] | M | Es el número de canales BSC. |
| [out] | HCOND | Es un vector con el resultado de evaluar las entropia condicionada para cada elemento del vector RHO. |
| int pds_symetric_joint_entropy_bsc_model | ( | double | rho, |
| PdsRaNatural | M, | ||
| double * | HJoint | ||
| ) |
Encuentra la entropia conjunta HJoint, 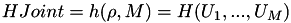 , de las señales a la salida de un bloque de de M fuentes binarias correlacionadas [2].
, de las señales a la salida de un bloque de de M fuentes binarias correlacionadas [2].
Este es el caso cuando todas las probabilidades de error son iguales a rho 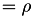 .
.

Dadas M fontes Um , m ={1,2,...,M}, generadas pasando una fuente U0, con probabilidade Pr(U0=1)=0.5, atraves de M canales BSC con probabilidades de error Ps=[rho, rho, ..., rho].
![\[ P_k(\rho,M)= 0.5 \{ \rho^k (1-\rho)^{M-k} + \rho^{M-k} (1-\rho)^{k} \} \]](form_40.png)
![\[ h(\rho,M)= \sum_{k=0}^{M} {M \choose k} P_k(\rho,M)~log_2 ( P_k(\rho,M) ) \]](form_41.png)
![\[ P(U_m \neq U_0| U_0)=\rho \]](form_32.png)
| [in] | rho | Es la probabilidad de error de los canales BSC. 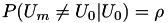 . . |
| [in] | M | Es el número de canales BSC. |
| [out] | HJoint | Entropia conjunta. 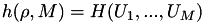 . . |
| int pds_inv_symetric_entropy_u0_omega_bsc_model | ( | double | HCond, |
| short int | M, | ||
| double * | rho | ||
| ) |
Encuentra la inversa 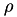 de la entropia condicionada HCond [4] .
de la entropia condicionada HCond [4] . 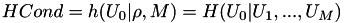 .
.
Esta funcion es la inversa de pds_symetric_entropy_u0_omega_bsc_model(). Cuando HCond y M son entregados la funcion retorna el valor de rho. Este es el caso cuando todas las probabilidades de error son iguales a rho. 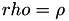 .
.

Dadas M fontes Um , m ={1,2,...,M}, generadas pasando una fuente U0, con probabilidade Pr(U0=1)=0.5, atraves de M canales BSC con probabilidades de error Ps=[rho, rho, ..., rho].
![\[ h(U_0| \rho,M)= \sum_{k=0}^{M} {M \choose k} \rho^k (1-\rho)^{M-k}~log_2 \left ( 1 + \{ \frac{\rho}{1-\rho} \}^{M-2 k} \right ) \]](form_31.png)
![\[ P(U_m \neq U_0| U_0)=\rho \]](form_32.png)
| [in] | HCond | Entropia condicionada. 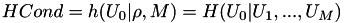 . . |
| [in] | M | Es el número de canales BSC. |
| [out] | rho | Es la probabilidad de error de los canales BSC. 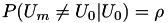 . . |
| int pds_inv_symetric_joint_entropy_bsc_model | ( | double | HJoint, |
| short int | M, | ||
| double * | rho | ||
| ) |
Encuentra la inversa 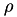 de la entropia conjunta
de la entropia conjunta 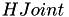 [2] .
[2] . 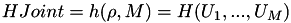 .
.
Esta funcion es la inversa de pds_symetric_joint_entropy_bsc_model(). Cuando HJoint y M son entregados la funcion retorna el valor de rho. Este es el caso cuando todas las probabilidades de error son iguales a rho 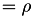 .
.

Dadas M fontes Um , m ={1,2,...,M}, generadas pasando una fuente U0, con probabilidade Pr(U0=1)=0.5, atraves de M canales BSC con probabilidades de error Ps=[rho, rho, ..., rho].
![\[ P_k(\rho,M)= 0.5 \{ \rho^k (1-\rho)^{M-k} + \rho^{M-k} (1-\rho)^{k} \} \]](form_40.png)
![\[ h(\rho,M)= \sum_{k=0}^{M} {M \choose k} P_k(\rho,M)~log_2 ( P_k(\rho,M) ) \]](form_41.png)
![\[ P(U_m \neq U_0| U_0)=\rho \]](form_32.png)
| [in] | HJoint | Entropia conjunta. 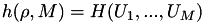 . . |
| [in] | M | Es el número de canales BSC. |
| [out] | rho | Es la probabilidad de error de los canales BSC. 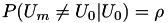 . . |
 1.8.6
1.8.6