

This module defines the Formex class, which is the major class for representing geometry in pyFormex. The Formex class implements most functionality of Formex algebra in a consistent and easy to understand syntax.
Classes defined in module formex
A structured collection of points in 3D space.
A Formex is a collection of points in the 3D space, that are structured into a set of elements all having the same number of points (e.g. a collection of line segments or a collection of triangles.)
The Formex basically contains (in its coords attribute) a Coords object, which is a Float type array with 3 axes (numbered 0,1,2). A scalar element of this array represents a coordinate.
A row along the last axis (2) is a set of coordinates and represents a point (aka. node, vertex). For simplicity’s sake, the current implementation only deals with points in a 3-dimensional space. This means that the length of axis 2 is always 3. The user can create Formices (plural of Formex) in a 2-D space, but internally these will be stored with 3 coordinates, by adding a third value 0. All operations work with 3-D coordinate sets. However, a method exists to extract only a limited set of coordinates from the results, permitting to return to a 2-D environment
A plane along the axes 2 and 1 is a set of points or element. This can be thought of as a geometrical shape (2 points form a line segment, 3 points make a triangle, ...) or as an element in Finite Element terms. But it really is up to the user as to how this set of points is to be interpreted.
Finally, the whole Formex represents a collection of such elements.
Additionally, a Formex may have a property set, which is an 1-D array of integers. The length of the array is equal to the length of axis 0 of the Formex data (i.e. the number of elements in the Formex). Thus, a single integer value may be attributed to each element. It is up to the user to define the use of this integer (e.g. it could be an index in a table of element property records). If a property set is defined, it will be copied together with the Formex data whenever copies of the Formex (or parts thereof) are made. Properties can be specified at creation time, and they can be set, modified or deleted at any time. Of course, the properties that are copied in an operation are those that exist at the time of performing the operation.
The Formex data can be initialized by another Formex, by a 2D or 3D coordinate list, or by a string to be used in one of the pattern functions to create a coordinate list. If 2D coordinates are given, a 3-rd coordinate 0.0 is added. Internally, Formices always work with 3D coordinates. Thus:
F = Formex([[[1,0],[0,1]],[[0,1],[1,2]]])
creates a Formex with two elements, each having 2 points in the global z-plane. The innermost level of brackets group the coordinates of a point, the next level groups the points in an element, and the outermost brackets group all the elements of the Formex. Because the coordinates are stored in an array with 3 axes, all the elements in a Formex must contain the same number of points. This number is called the plexitude of the Formex.
A Formex may be initialized with a string instead of the numerical coordinate data. The string has the format #:data where # is a leader specifying the plexitude of the elements to be created. The data part of the string is passed to the coords.pattern() function to generate a list of points on a regular grid of unit distances. Then the generated points are grouped in elements. If # is a number it just specifies the plexitude:
F = Formex('3:012034')
This creates six points, grouped by 3, thus leading to two elements (triangles). The leader can als be the character l. In that case each generated point is turned into a 2-point (line) element, by connecting it to the previous point. The following are two equivalent definitions of (the circumference of) a triangle:
F = Formex('2:010207')
G = Formex('l:127')
The Formex constructor takes two optional arguments: prop and eltype. If a prop argument is specified, the setProp() function will be called to assign the specified properties. eltype can be used to specify a non-default element type. The default element type is derived from the plexitude as follows: 1 = point, 2 = line segment, 3 = triangle, 4 or more is a polygon. Specifying eltype = 'tet4' will e.g. interprete 4 point elements as a tetraeder.
Because the Formex class is derived from Geometry, the following Formex methods exist and return the value of the same method applied on the coords attribute: x, y, z, bbox, center, centroid, sizes, dsize, bsphere, distanceFromPlane, distanceFromLine, distanceFromPoint, directionalSize, directionalWidth, directionalExtremes, __str__. Refer to the correponding Coords method for their usage.
Also, the following Coords transformation methods can be directly applied to a Formex object or a derived class object. The return value is a new object identical to the original, except for the coordinates, which will have been transformed by the specified method. Refer to the correponding Coords method for the usage of these methods: scale, translate, rotate, shear, reflect, affine, cylindrical, hyperCylindrical, toCylindrical, spherical, superSpherical, toSpherical, bump, bump1, bump2, flare, map, map1, mapd, newmap, replace, swapAxes, rollAxes, projectOnSphere, projectOnCylinder, rot, trl.
Return element i of the Formex
Return point j of element i
Return coord k of point j of element i
Return the number of elements in the formex.
Return the number of points per element.
Examples:
Return the number of dimensions.
This is the number of coordinates for each point. In the current implementation this is always 3, though you can define 2D Formices by given only two coordinates: the third will automatically be set to zero.
Return the number of points in the formex.
This is the product of the number of elements in the formex with the number of nodes per element.
Return the level (dimensionality) of the Formex.
The level or dimensionality of a geometrical object is the minimum number of parametric directions required to describe the object. Thus we have the following values:
0: points 1: lines 2: surfaces 3: volumes
Because the geometrical meaning of a Formex is not always defined, the level may be unknown. In that case, -1 is returned.
If the Formex has an ‘eltype’ set, the value is determined from the Element database. Else, the value is equal to the plexitude minus one for plexitudes up to 3, an equal to 2 for any higher plexitude (since the default is to interprete a higher plexitude as a polygon).
Return the Formex coordinates as a numpy array (ndarray).
Since the ndarray object has a method view() returning a view on the ndarray, this method allows writing code that works with both Formex and ndarray instances. The results is always an ndarray.
Return the property numbers of the element in index
Return the highest property value used, or None
Return a list with unique property values on this Formex.
Return the centroids of all elements of the Formex.
The centroid of an element is the point whose coordinates are the mean values of all points of the element. The return value is a Coords object with nelems points.
Return a tuple of nodal coordinates and element connectivity.
A tuple of two arrays is returned. The first is float array with the coordinates of the unique nodes of the Formex. The second is an integer array with the node numbers connected by each element. The elements come in the same order as they are in the Formex, but the order of the nodes is unspecified. By the way, the reverse operation of coords,elems=fuse(F) is accomplished by F=Formex(coords[elems])
There is a (very small) probability that two very close nodes are not equivalenced by this procedure. Use it multiple times with different parameters to check. You can also set the rtol/atol parameters to influence the equivalence checking of two points. The default settting for atol is rtol * self.dsize()
Convert a Formex to a Mesh.
Converts a geometry in Formex model to the equivalent Mesh model. In the Mesh model, all points with nearly identical coordinates are fused into a single point, and elements are defined by a connectivity table with integers pointing to the corresponding vertex.
Convert a Formex to a Surface.
Tries to convert the Formex to a TriSurface. First the Formex is converted to a Mesh, and then the resulting Mesh is converted to a TriSurface.
The conversion will only work if the Formex represents a surface and its elements are triangles or quadrilaterals.
Returns a TriSurface if the conversion succeeds, else an error is raised. If the plexitude of the Formex is 3, the returned TriSurface is equivalent with the Formex.
Return formatted information about a Formex.
Return a string representation of a point
Return a string representation of an element
Return string representation of a Formex as in Formian.
Coordinates are separated by commas, points are separated by semicolons and grouped between brackets, elements are separated by commas and grouped between braces:
>>> F = Formex([[[1,0],[0,1]],[[0,1],[1,2]]])
>>> print(F)
{[1.0,0.0,0.0; 0.0,1.0,0.0], [0.0,1.0,0.0; 1.0,2.0,0.0]}
Return string representation as Formex with properties.
The string representation as done by asFormex() is followed by the words “with prop” and a list of the properties.
Return string representation as a numpy array.
Choose the default formatting for printing formices.
This sets how formices will be formatted by a print statement. Currently there are two available functions: asFormex, asArray. The user may create its own formatting method. This is a class method. It should be used asfollows: Formex.setPrintFunction(Formex.asArray).
Append the members of Formex F to this one.
This function changes the original one! Use __add__ if you want to get a copy with the sum.
>>> F = Formex([[[1.0,1.0,1.0]]])
>>> G = F.append(F)
>>> print(F)
{[1.0,1.0,1.0], [1.0,1.0,1.0]}
Concatenate all Formices in Flist.
All the Formices in the list should have the same plexitude, If any of the Formices has property numbers, the resulting Formex will inherit the properties. In that case, any Formices without properties will be assigned property 0. If all Formices are without properties, so will be the result. The eltype of the resulting Formex will be that of the first Formex in the list.
This is a class method, not an instance method!
>>> F = Formex([[[1,2,3]]],1)
>>> print(Formex.concatenate([F,F,F]))
{[1.0,2.0,3.0], [1.0,2.0,3.0], [1.0,2.0,3.0]}
Formex.concatenate([F,G,H]) is functionally equivalent with F+G+H. The latter is simpler to write for a list with a few elements. If the list becomes large, or the number of items in the list is not fixed, the concatenate method is easier (and faster). We made it a class method and not a global function, because that would interfere with NumPy’s own concatenate function.
Return a Formex with only the elements selected by the parameter.
The parameter idx can be
See cselect() for the complementary operation.
Return a Formex without the elements selected by the parameter.
The parameter idx can be
This is the complementary operation of select()
Return a Formex which holds only some nodes of the parent.
idx is a list of node numbers to select. Thus, if F is a plex 3 Formex representing triangles, the sides of the triangles are given by F.selectNodes([0,1]) + F.selectNodes([1,2]) + F.selectNodes([2,0]) The returned Formex inherits the property of its parent.
Return a Formex containing only the points.
This is obviously a Formex with plexitude 1. It holds the same data as the original Formex, but in another shape: the number of points per element is 1, and the number of elements is equal to the total number of points. The properties are not copied over, since they will usually not make any sense.
The points() method returns the same data, but as a Coords object with a simple list of points.
Return a Formex where the elements in F have been removed.
This is also the subtraction of the current Formex with F. Elements are only removed if they have the same nodes in the same order. This is a slow operation: for large structures, you should avoid it where possible.
Return the numbers of the elements with property val.
val is either a single integer, or a list/array of integers. The return value is an array holding all the numbers of all the elements that have the property val, resp. one of the values in val.
If the Formex has no properties, a empty array is returned.
Return a Formex which holds only the elements with property val.
val is either a single integer, or a list/array of integers. The return value is a Formex holding all the elements that have the property val, resp. one of the values in val. The returned Formex inherits the matching properties.
If the Formex has no properties, a copy with all elements is returned.
Return a Formex where each element is replaced by its bbox.
The returned Formex has two points for each element: the two corners of the bbox with the minimal and maximal coordinates.
Return a Formex which holds only the unique elements.
Two elements are considered equal when all its points are (nearly) coincident. By default any permutation of point order is also allowed.
Two coordinate value are considered equal if they are both small compared to atol or if their difference divided by the second value is small compared to rtol.
If permutations is set False, two elements are not considered equal if one’s points are a permutation of the other’s.
Return a Formex which holds only the unique elements.
Two elements are considered equal when all its points are (nearly) coincident. By default any permutation of point order is also allowed.
Two coordinate value are considered equal if they are both small compared to atol or if their difference divided by the second value is small compared to rtol.
If permutations is set False, two elements are not considered equal if one’s points are a permutation of the other’s.
Flag elements having nodal coordinates between min and max.
This function is very convenient in clipping a Formex in a specified direction. It returns a 1D integer array flagging (with a value 1 or True) the elements having nodal coordinates in the required range. Use where(result) to get a list of element numbers passing the test. Or directly use clip() or cclip() to create the clipped Formex.
The test plane can be defined in two ways, depending on the value of dir. If dir==0, 1 or 2, it specifies a global axis and min and max are the minimum and maximum values for the coordinates along that axis. Default is the 0 (or x) direction.
Else, dir should be compaitble with a (3,) shaped array and specifies the direction of the normal on the planes. In this case, min and max are points and should also evaluate to (3,) shaped arrays.
nodes specifies which nodes are taken into account in the comparisons. It should be one of the following: - a single (integer) point number (< the number of points in the Formex) - a list of point numbers - one of the special strings: ‘all’, ‘any’, ‘none’ The default (‘all’) will flag all the elements that have all their nodes between the planes x=min and x=max, i.e. the elements that fall completely between these planes. One of the two clipping planes may be left unspecified.
Return a Formex with all the elements where t>0.
t should be a 1-D integer array with length equal to the number of elements of the formex. The resulting Formex will contain all elements where t > 0. This is a convenience function for the user, equivalent to F.select(t>0).
This is the complement of clip, returning a Formex where t<=0.
Transform a linear sector into a circular one.
A sector of the (0,1) plane with given angle, starting from the 0 axis, is transformed as follows: points on the sector borders remain in place. Points inside the sector are projected from the center on the circle through the intersection points of the sector border axes and the line through the point and perpendicular to the bisector of the angle. See Diamatic example.
Transforms the first octant of the 0-1 plane into 1/6 of a circle.
Points on the 0-axis keep their position. Lines parallel to the 1-axis are transformed into circular arcs. The bisector of the first quadrant is transformed in a straight line at an angle Pi/6. This function is especially suited to create circular domains where all bars have nearly same length. See the Diamatic example.
Shrinks each element with respect to its own center.
Each element is scaled with the given factor in a local coordinate system with origin at the element center. The element center is the mean of all its nodes. The shrink operation is typically used (with a factor around 0.9) in wireframe draw mode to show all elements disconnected. A factor above 1.0 will grow the elements.
Return a Formex where all elements have been reversed.
Reversing an element means reversing the order of its points. This is equivalent to:
self.selectNodes(arange(self.nplex()-1,-1,-1))
Reflect a Formex in one of the coordinate directions
This method behaves like reflect(), but adds the reflected part to the original. Setting keep_orig=False makes it behave just like reflect().
Replicate a Formex n times with fixed step in any direction.
Returns a Formex which is the concatenation of n copies, where each copy is equal to the previous one translated over (dir,step), where dir and step are interpreted just like in the translate() method. The first of the copies is equal to the original.
Like replicate, but allow repeated replication
n, dir and step are lists. Default values for dir are [0,1,2] and [1.0,1.0,1.0], cutoff at the length of the specified n.
Return a Formex with n replications in direction dir with step.
The original Formex is the first of the n replicas.
Replicate in two directions.
n1,n2 number of replications with steps t1,t2 in directions d1,d2 bias, taper : extra step and extra number of generations in direction d1 for each generation in direction d2
Return a Formex with n rotational replications with angular step angle around an axis parallel with one of the coordinate axes going through the given point. axis is the number of the axis (0,1,2). point must be given as a list (or array) of three coordinates. The original Formex is the first of the n replicas.
Return a Formex with n rotational replications with angular step angle around an axis parallel with one of the coordinate axes going through the given point. axis is the number of the axis (0,1,2). point must be given as a list (or array) of three coordinates. The original Formex is the first of the n replicas.
Multiple subsequent translations in axis directions.
The argument list is a sequence of tuples (axis, step). Thus translatem((0,x),(2,z),(1,y)) is equivalent to translate([x,y,z]). This function is especially conveniant to translate in calculated directions.
Extrude a Formex in one of the axis directions.
Returns a Formex with doubled plexitude.
First the original Formex is translated over n steps of length step in direction dir. Then each pair of subsequent Formices is connected to form a higher plexitude structure.
Currently, this function correctly transforms: point1 to line2, line2 to quad4, tri3 to wedge6, quad4 to hex8.
See the ‘connect’ function for a more versatile tool.
Divide a plex-2 Formex at the values in div.
Replaces each member of the Formex by a sequence of members obtained by dividing the Formex at the relative values specified in div. The values should normally range from 0.0 to 1.0.
As a convenience, if an integer is specified for div, it is taken as a number of divisions for the interval [0..1].
This function only works on plex-2 Formices (line segments).
Return the intersection of a Formex with the plane (p,n) within tolerance atol.
Currently this only works for plex-2 and plex-3 Formices.
The intersection of the Formex with a plane specified by a point p and normal n is returned. For a plex-2 Formex (lines), the returned Formex will be of plexitude 1 (points). For a plex-3 Formex (triangles) the returned Formex has plexitude 2 (lines).
Cut a Formex with the plane(s) (p,n).
Warning
This method currently only works for plexitude 2 or 3!
Parameters:
Returns:
The default return value is a tuple of two Formices of the same plexitude as the input: (Fpos,Fneg), where Fpos is the part of the Formex at the positive side of the plane (as defined by the normal vector), and Fneg is the part at the negative side. Elements of the input Formex that are lying completely on one side of the plane will return unaltered. Elements that are crossing the plane will be cut and split up into multiple parts.
When side = ‘+’ or ‘-‘ (or ‘positive’or ‘negative’), only one of the sides is returned.
Split a Formex in subFormices containing n elements.
The number of elements in the Formex should be a multiple of n. Returns a list of Formices each comprising n elements.
Compute the length of all elements of a 2-plex Formex.
The length of an element is the distance between its two points.
Compute the areas of all elements of a 3-plex Formex.
The area of an element is the aread of the triangle formed by its three points.
Compute the volume of all elements of a 4-plex Formex.
The volume of an element is the volume of the tetraeder formed by its points.
Write a Formex to file.
If fil is a string, a file with that name is opened. Else fil should be an open file. The Formex is then written to that file in a native format, using sep as separator between the coordinates. If fil is a string, the file is closed prior to returning.
Read a Formex from file.
fil is a filename or a file object. If the file is in a valid Formex file format, the Formex is read and returned. Otherwise, None is returned. Valid Formex file formats are described in the manual.
Create a Formex from coodinates in a string.
This uses the Coords.fromstring() method to read coordinates from a string and restructures them into a Formex of the specified plexitude.
Parameters:
The return value is a Coords object.
Read the coordinates of a Formex from a file
Apply ‘addNoise’ transformation to the Geometry object.
See coords.Coords.addNoise() for details.
Apply ‘affine’ transformation to the Geometry object.
See coords.Coords.affine() for details.
Apply ‘align’ transformation to the Geometry object.
See coords.Coords.align() for details.
Apply ‘bump’ transformation to the Geometry object.
See coords.Coords.bump() for details.
Apply ‘bump1’ transformation to the Geometry object.
See coords.Coords.bump1() for details.
Apply ‘bump2’ transformation to the Geometry object.
See coords.Coords.bump2() for details.
Apply ‘centered’ transformation to the Geometry object.
See coords.Coords.centered() for details.
Apply ‘cylindrical’ transformation to the Geometry object.
See coords.Coords.cylindrical() for details.
Apply ‘egg’ transformation to the Geometry object.
See coords.Coords.egg() for details.
Apply ‘flare’ transformation to the Geometry object.
See coords.Coords.flare() for details.
Apply ‘hyperCylindrical’ transformation to the Geometry object.
See coords.Coords.hyperCylindrical() for details.
Apply ‘isopar’ transformation to the Geometry object.
See coords.Coords.isopar() for details.
Apply ‘map’ transformation to the Geometry object.
See coords.Coords.map() for details.
Apply ‘map1’ transformation to the Geometry object.
See coords.Coords.map1() for details.
Apply ‘mapd’ transformation to the Geometry object.
See coords.Coords.mapd() for details.
Apply ‘position’ transformation to the Geometry object.
See coords.Coords.position() for details.
Apply ‘projectOnCylinder’ transformation to the Geometry object.
See coords.Coords.projectOnCylinder() for details.
Apply ‘projectOnPlane’ transformation to the Geometry object.
See coords.Coords.projectOnPlane() for details.
Apply ‘projectOnSphere’ transformation to the Geometry object.
See coords.Coords.projectOnSphere() for details.
Apply ‘reflect’ transformation to the Geometry object.
See coords.Coords.reflect() for details.
Apply ‘replace’ transformation to the Geometry object.
See coords.Coords.replace() for details.
Apply ‘rollAxes’ transformation to the Geometry object.
See coords.Coords.rollAxes() for details.
Apply ‘rotate’ transformation to the Geometry object.
See coords.Coords.rotate() for details.
Apply ‘rotate’ transformation to the Geometry object.
See coords.Coords.rotate() for details.
Apply ‘scale’ transformation to the Geometry object.
See coords.Coords.scale() for details.
Apply ‘shear’ transformation to the Geometry object.
See coords.Coords.shear() for details.
Apply ‘spherical’ transformation to the Geometry object.
See coords.Coords.spherical() for details.
Apply ‘superSpherical’ transformation to the Geometry object.
See coords.Coords.superSpherical() for details.
Apply ‘swapAxes’ transformation to the Geometry object.
See coords.Coords.swapAxes() for details.
Apply ‘toCylindrical’ transformation to the Geometry object.
See coords.Coords.toCylindrical() for details.
Apply ‘toSpherical’ transformation to the Geometry object.
See coords.Coords.toSpherical() for details.
Apply ‘transformCS’ transformation to the Geometry object.
See coords.Coords.transformCS() for details.
Apply ‘translate’ transformation to the Geometry object.
See coords.Coords.translate() for details.
Apply ‘translate’ transformation to the Geometry object.
See coords.Coords.translate() for details.
Create or destroy the property array for the Geometry.
A property array is a rank-1 integer array with dimension equal to the number of elements in the Geometry. Each element thus has its own property number. These numbers can be used for any purpose. They play an import role when creating new geometry: new elements inherit the property number of their parent element. Properties are also preserved on most geometrical transformations.
Because elements with different property numbers can be drawn in different colors, the property numbers are also often used to impose color.
Parameters:
prop: a single integer value or a list/array of integer values. If the number of passed values is less than the number of elements, they wil be repeated. If you give more, they will be ignored.
The special value ‘range’ will set the property numbers equal to the element number.
A value None (default) removes the properties from the Geometry.
blocks: a single integer value or a list/array of integer values. If the number of passed values is less than the length of prop, they wil be repeated. If you give more, they will be ignored. Every prop will be repeated the corresponding number of times specified in blocks.
Converts the argument into a legal set of properties for the object.
The conversion involves resizing the argument to a 1D array of length self.nelems(), and converting the data type to integer.
Get the coords data.
Returns the full array of coordinates stored in the Geometry object. Note that subclasses may store more points in this array than are used to define the geometry.
Return a deep copy of the Geometry object.
The returned object is an exact copy of the input, but has all of its data independent of the former.
Partition a Geometry (Formex/Mesh) according to the values in prop.
Parameters:
Returns a list of Geometry objects of the same type as the input. Each object contains all the elements having the same value of prop. The number of objects in the list is equal to the number of unique values in prop. The list is sorted in ascending order of their prop value.
It prop is None and the the object has no prop attribute, an empty list is returned.
Return the number of points in the formex.
This is the product of the number of elements in the formex with the number of nodes per element.
Return a copy of the Geometry scaled to the given size.
size can be a single value or a list of three values for the three coordinate directions. If it is a single value, all directions are scaled to the same size. Directions for which the geometry has a size smaller than tol times the maximum size are not rescaled.
Functions defined in module formex
Return a Formex which connects the Formices in list.
Flist is a list of formices, nodid is an optional list of nod ids and bias is an optional list of element bias values. All lists should have the same length. The returned Formex has a plexitude equal to the number of formices in list. Each element of the Formex consist of a node from the corresponding element of each of the formices in list. By default this will be the first node of that element, but a nodid list may be given to specify the node id to be used for each of the formices. Finally, a list of bias values may be given to specify an offset in element number for the subsequent formices. If loop==False, the order of the Formex will be the minimum order of the formices in Flist, each minus its respective bias. By setting loop=True however, each Formex will loop around if its end is encountered, and the order of the result is the maximum order in Flist.
Create interpolations between two formices.
F and G are two Formices with the same shape. div is a list of floating point values. The result is the concatenation of the interpolations of F and G at all the values in div. An interpolation of F and G at value v is a Formex H where each coordinate Hijk is obtained from: Hijk = Fijk + v * (Gijk-Fijk). Thus, a Formex interpolate(F,G,[0.,0.5,1.0]) will contain all elements of F and G and all elements with mean coordinates between those of F and G.
As a convenience, if an integer is specified for div, it is taken as a number of divisions for the interval [0..1]. Thus, interpolate(F,G,n) is equivalent with interpolate(F,G,arange(0,n+1)/float(n))
The swap argument sets the order of the elements in the resulting Formex. By default, if n interpolations are created of an m-element Formex, the element order is in-Formex first (n sequences of m elements). If swap==True, the order is swapped and you get m sequences of n interpolations.
Return a line segment pattern created from a string.
This function creates a list of line segments where all points lie on a regular grid with unit step. The first point of the list is [0,0,0]. Each character from the input string is interpreted as a code specifying how to move to the next point. Currently defined are the following codes: 1..8 move in the x,y plane 9 remains at the same place 0 = goto origin [0,0,0] + = go back to origin without creating a line segment When looking at the plane with the x-axis to the right, 1 = East, 2 = North, 3 = West, 4 = South, 5 = NE, 6 = NW, 7 = SW, 8 = SE. Adding 16 to the ordinal of the character causes an extra move of +1 in the z-direction. Adding 48 causes an extra move of -1. This means that ‘ABCDEFGHI’, resp. ‘abcdefghi’, correspond with ‘123456789’ with an extra z +/-= 1. This gives the following schema:
z+=1 z unchanged z -= 1
F B E 6 2 5 f b e
| | |
| | |
C----I----A 3----9----1 c----i----a
| | |
| | |
G D H 7 4 8 g d h
The special character ‘/’ can be put before any character to make the move without inserting an element. The effect of any other character is undefined.
The resulting list is directly suited to initialize a Formex.
Return the points of a plex-2 Formex at times t.
F is a plex 2 Formex and t is an array with F.nelems() float values which are interpreted as local parameters along the edges of the Formex, such that the first node has value 0.0 and the last has value 1.0. The return value is a coords.Coords array with the points at values t.
Return the intersection lines of a plex-3 Formex with plane (p,n).
F is a Formex of plexitude 3. p is a point specified by 3 coordinates. n is the normal vector to a plane, specified by 3 components. atol is a tolerance factor defining whether an edge is intersected by the plane.
Returns all elements of the Formex cut at plane.
F is a Formex of plexitude 2. p is a point specified by 3 coordinates. n is the normal vector to a plane, specified by 3 components.
The return value is:
To avoid roundoff errors and creation of very small elements, a tolerance can be specified. Points lying within the tolerance distance will be considered lying in the plane, and no cutting near these points.
Returns all elements of the Formex cut at plane(s).
F is a Formex of plexitude 3. p is a point or a list of points. n is the normal vector to a plane or a list of normal vectors. Both p and n have shape (3) or (npoints,3).
The return value is:
Let 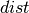 be the signed distance of the vertices to a plane.
The elements located completely at the positive or negative side of
a plane have three vertices for which
be the signed distance of the vertices to a plane.
The elements located completely at the positive or negative side of
a plane have three vertices for which 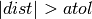 .
The elements intersecting a plane can have one or more vertices for which
.
The elements intersecting a plane can have one or more vertices for which
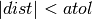 .
These vertices are projected on the plane so that their distance is zero.
.
These vertices are projected on the plane so that their distance is zero.
If the Formex has a property set, the new elements will get the property numbers defined in newprops. This is a list of 7 property numbers flagging elements with following properties:
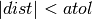 , triangle after cut
, triangle after cut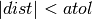 , triangle 1 from quad after cut
, triangle 1 from quad after cut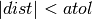 , triangle 2 from quad after cut
, triangle 2 from quad after cut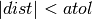 , two vertices at pos. or neg. side
, two vertices at pos. or neg. side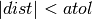 , one vertex at pos. side, one at neg.
, one vertex at pos. side, one at neg.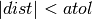 , one vertex at pos. or neg. side
, one vertex at pos. or neg. side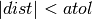
This function needs documentation.
Should it be called by the user? or only via cut3AtPlane? For now, lets suppose the last, so no need to check arguments here.
newprops should be a list of 7 values: each an integer or None side is either ‘+’, ‘-‘ or ‘’