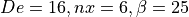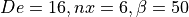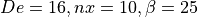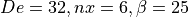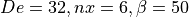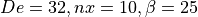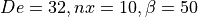pyFormex example scripts¶
Warning
This document still needs some cleanup!
Sometimes you learn quicker from studying an example than from reading a tutorial or user guide. To help you we have created this collection of annotated examples. Beware that the script texts presented in this document may differ slightly from the corresponding example coming with the pyFormex distribution.
WireStent¶
To get acquainted with the modus operandi of pyFormex,
the WireStent.py script is studied step by step. The lines are numbered
for easy referencing, but are not part of the script itself.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 | # *** pyformex ***
##
## This file is part of pyFormex 1.0.7 (Mon Jun 17 12:20:39 CEST 2019)
## pyFormex is a tool for generating, manipulating and transforming 3D
## geometrical models by sequences of mathematical operations.
## Home page: http://pyformex.org
## Project page: http://savannah.nongnu.org/projects/pyformex/
## Copyright 2004-2019 (C) Benedict Verhegghe (benedict.verhegghe@ugent.be)
## Distributed under the GNU General Public License version 3 or later.
##
## This program is free software: you can redistribute it and/or modify
## it under the terms of the GNU General Public License as published by
## the Free Software Foundation, either version 3 of the License, or
## (at your option) any later version.
##
## This program is distributed in the hope that it will be useful,
## but WITHOUT ANY WARRANTY; without even the implied warranty of
## MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
## GNU General Public License for more details.
##
## You should have received a copy of the GNU General Public License
## along with this program. If not, see http://www.gnu.org/licenses/.
##
"""Wirestent.py
A pyFormex script to generate a geometrical model of a wire stent.
This version is for inclusion in the pyFormex documentation.
"""
from formex import *
class DoubleHelixStent:
"""Constructs a double helix wire stent.
A stent is a tubular shape such as used for opening obstructed
blood vessels. This stent is made frome sets of wires spiraling
in two directions.
The geometry is defined by the following parameters:
L : approximate length of the stent
De : external diameter of the stent
D : average stent diameter
d : wire diameter
be : pitch angle (degrees)
p : pitch
nx : number of wires in one spiral set
ny : number of modules in axial direction
ds : extra distance between the wires (default is 0.0 for
touching wires)
dz : maximal distance of wire center to average cilinder
nb : number of elements in a strut (a part of a wire between two
crossings), default 4
The stent is created around the z-axis.
By default, there will be connectors between the wires at each
crossing. They can be switched off in the constructor.
The returned formex has one set of wires with property 1, the
other with property 3. The connectors have property 2. The wire
set with property 1 is winding positively around the z-axis.
"""
def __init__(self,De,L,d,nx,be,ds=0.0,nb=4,connectors=True):
"""Create the Wire Stent."""
D = De - 2*d - ds
r = 0.5*D
dz = 0.5*(ds+d)
p = math.pi*D*tand(be)
nx = int(nx)
ny = int(round(nx*L/p)) # The actual length may differ a bit from L
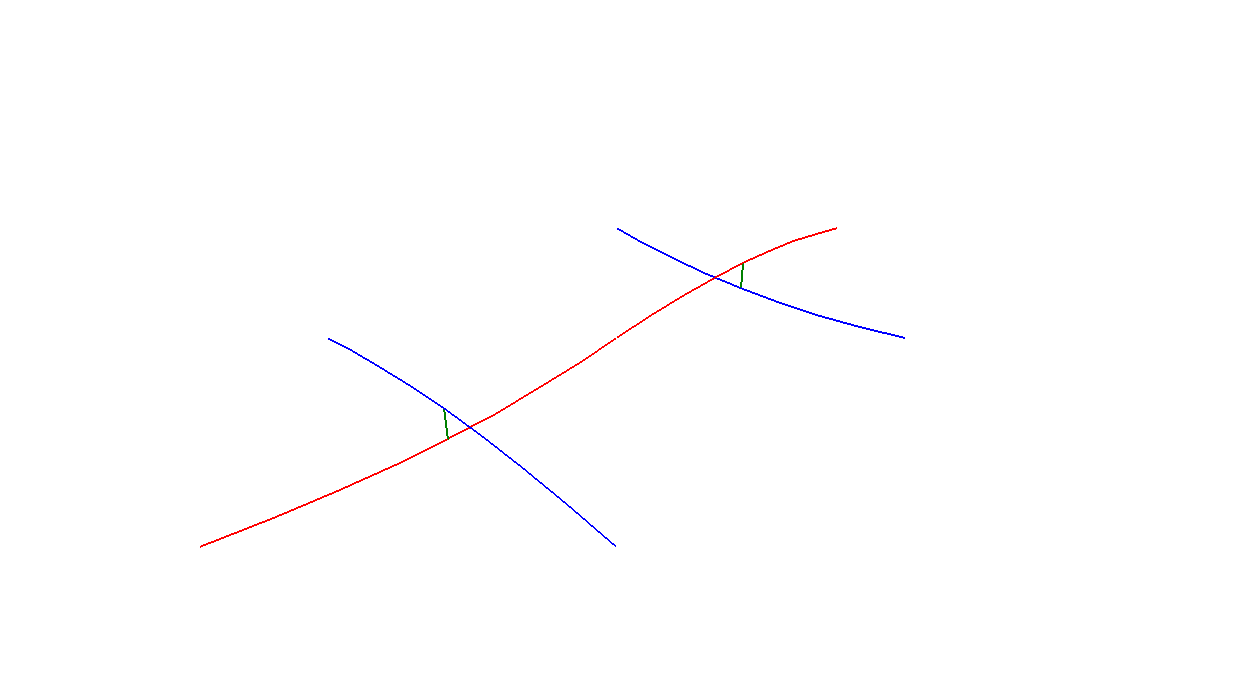
# a single bumped strut, oriented along the x-axis
bump_z=lambda x: 1.-(x/nb)**2
base = Formex(pattern('1')).replic(nb,1.0).bump1(2,[0.,0.,dz],bump_z,0)
# scale back to size 1.
base = base.scale([1./nb,1./nb,1.])
# NE and SE directed struts
NE = base.shear(1,0,1.)
SE = base.reflect(2).shear(1,0,-1.)
NE.setProp(1)
SE.setProp(3)
# a unit cell of crossing struts
cell1 = (NE+SE).rosette(2,180)
# add a connector between first points of NE and SE
if connectors:
cell1 += Formex([[NE[0][0],SE[0][0]]],2)
# and create its mirror
cell2 = cell1.reflect(2)
# and move both to appropriate place
self.cell1 = cell1.translate([1.,1.,0.])
self.cell2 = cell2.translate([-1.,-1.,0.])
# the base pattern cell1+cell2 now has size [-2,-2]..[2,2]
# Create the full pattern by replication
dx = 4.
dy = 4.
F = (self.cell1+self.cell2).replic2(nx,ny,dx,dy)
# fold it into a cylinder
self.F = F.translate([0.,0.,r]).cylindrical(
dir=[2,0,1],scale=[1.,360./(nx*dx),p/nx/dy])
self.ny = ny
def all(self):
"""Return the Formex with all bar elements."""
return self.F
if __name__ == "draw":
# show an example
wireframe()
reset()
D = 10.
L = 80.
d = 0.2
n = 12
b = 30.
res = askItems([['Diameter',D],
['Length',L],
['WireDiam',d],
['NWires',n],
['Pitch',b]])
if not res:
exit()
D = float(res['Diameter'])
L = float(res['Length'])
d = float(res['WireDiam'])
n = int(res['NWires'])
if (n % 2) != 0:
warning('Number of wires must be even!')
exit()
b = float(res['Pitch'])
H = DoubleHelixStent(D,L,d,n,b).all()
clear()
draw(H,view='iso')
# and save it in a lot of graphics formats
if ack("Do you want to save this image (in lots of formats) ?"):
for ext in [ 'bmp', 'jpg', 'pbm', 'png', 'ppm', 'xbm', 'xpm',
'eps', 'ps', 'pdf', 'tex' ]:
image.save('WireStent.'+ext)
# End
|
As all pyFormex scripts, it starts with a comments line holding the word
pyformex (line 1). This is followed more comments lines specifying the
copyright and license notices. If you intend to distribute your scripts, you should give these certainly special consideration.
Next is a documentation string explaining
the purpose of the script (lines 25-30).
The script then starts by importing all definitions from
other modules required to run the WireStent.py
script (line 32).
Subsequently, the class DoubleHelixStent is defined which
allows the simple use of the geometrical model in other scripts for e.g.
parametric, optimization and finite element analyses of braided wire stents.
Consequently, the latter scripts do not have to contain the wire stent geometry
building and can be condensed and conveniently arranged. The definition of the
class starts with a documentation string, explaining
its aim and functioning (lines 34-60).
The constructor __init__ of the DoubleHelixStent class requires 8
arguments (line 61):
- stent external diameter
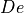 (mm).
(mm). - stent length
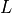 (mm).
(mm). - wire diameter
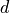 (mm).
(mm). - Number of wires in one spiral set, i.e. wires with the same orientation,
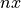 (-).
(-). - Pitch angle
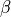 (
(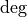 ).
). - Extra radial distance between the crossing wires
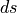 (mm). By default,
(mm). By default,
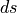 is [0.0]mm for crossing wires, corresponding with a centre line
distance between two crossing wires of exactly
is [0.0]mm for crossing wires, corresponding with a centre line
distance between two crossing wires of exactly 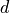 .
. - Number of elements in a strut, i.e. part of a wire between two crossings,
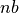 (-). As every base element is a straight line, multiple elements are
required to approximate the curvature of the stent wires. The default value of 4
elements in a strut is a good assumption.
(-). As every base element is a straight line, multiple elements are
required to approximate the curvature of the stent wires. The default value of 4
elements in a strut is a good assumption. - If
connectors=True, extra elements are created at the positions where there is physical contact between the crossing wires. These elements are required to enable contact between these wires in finite element analyses.
The virtual construction of the wire stent structure is defined by the following sequence of four operations: (i) Creation of a nearly planar base module of two crossing wires; (ii) Extending the base module with a mirrored and translated copy; (iii) Replicating the extended base module in both directions of the base plane; and (iv) Rolling the nearly planar grid into the cylindrical stent structure, which is easily parametric adaptable.
Creating the base module¶
(lines 63-71)
Depending on the specified arguments in the constructor, the mean stent diameter
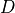 , the average stent radius
, the average stent radius  , the
, the bump or curvature of the
wires 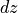 , the pitch
, the pitch 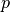 and the number of base modules in the
axial direction
and the number of base modules in the
axial direction 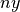 are calculated with the following script. As the wire
stent structure is obtained by braiding, the wires have an undulating course and
the
are calculated with the following script. As the wire
stent structure is obtained by braiding, the wires have an undulating course and
the bump dz corresponds to the amplitude of the wave. If no extra distance
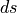 is specified, there will be exactly one wire diameter between the
centre lines of the crossing wires. The number of modules in the axial direction
is specified, there will be exactly one wire diameter between the
centre lines of the crossing wires. The number of modules in the axial direction
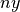 is an integer, therefore, the actual length of the stent model might
differ slightly from the specified, desired length
is an integer, therefore, the actual length of the stent model might
differ slightly from the specified, desired length 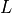 . However, this
difference has a negligible impact on the numerical results.
. However, this
difference has a negligible impact on the numerical results.
Of now, all parameters to describe the stent geometry are specified and
available to start the construction of the wire stent. Initially a simple Formex
is created using the pattern()-function: a straigth line segment of length
1 oriented along the X-axis (East or 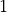 -direction). The
-direction). The replic()-functionality replicates this line segment 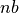 times with step 1 in the
X-direction (
times with step 1 in the
X-direction ( -direction). Subsequently, these
-direction). Subsequently, these 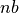 line
segments form a new Formex which is given a one-dimensional
line
segments form a new Formex which is given a one-dimensional bump with the
bump1()-function. The Formex undergoes a deformation in the Z-direction
(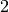 -direction), forced by the point
-direction), forced by the point [0,0,dz]. The bump
intensity is specified by the quadratic bump_z function and varies along the
X-axis ( -axis). The creation of this single bumped strut, oriented
along the X-axis is summarized in the next script and depicted in figures
A straight line segment, The line segment with replications and A bumped line segment,.
-axis). The creation of this single bumped strut, oriented
along the X-axis is summarized in the next script and depicted in figures
A straight line segment, The line segment with replications and A bumped line segment,.
The single bumped strut (base) is rescaled homothetically in the XY-plane to
size one with the scale()-function. Subsequently, the shear()-functionality generates a new NE Formex by skewing the base Formex in
the Y-direction (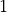 -direction) with a
-direction) with a skew factor of 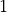 in
the YX-plane. As a result, the Y-coordinates of the
in
the YX-plane. As a result, the Y-coordinates of the base Formex are altered
according to the following rule: 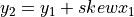 . Similarly a
. Similarly a
SE Formex is generated by a shear() operation on a mirrored copy of the
base Formex. The base copy, mirrored in the direction of the XY-plane
(perpendicular to the 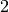 -axis), is obtained by the
-axis), is obtained by the reflect()
command. Both Formices are given a different property number by the
setProp()-function, visualised by the different color codes in Figure
Unit cell of crossing wires and connectors This number can be used as an entry in a database, which holds some
sort of property. The Formex and the database are two seperate entities, only
linked by the property numbers. The rosette()-function creates a unit cell
of crossing struts by 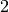 rotational replications with an angular step of
[180]:math:deg around the Z-axis (the original Formex is the first of the
rotational replications with an angular step of
[180]:math:deg around the Z-axis (the original Formex is the first of the
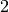 replicas). If specified in the constructor, an additional Formex with
property
replicas). If specified in the constructor, an additional Formex with
property 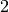 connects the first points of the
connects the first points of the NE and SE Formices.
(lines 72-83)
Extending the base module¶
Subsequently, a mirrored copy of the base cell is generated (Figure
Mirrored unit cell). Both Formices are
translated to their appropriate side by side position with the translate()-option and form the complete extended base module with 4 by 4 dimensions as
depicted in Figure Completed base module.
Furthermore, both Formices are defined as an
attribute of the DoubleHelixStent class by the self-statement,
allowing their use after every DoubleHelixStent initialisation. Such further
use is impossible with local variables, such as for example the NE and
SE Formices.
(lines 84-89)
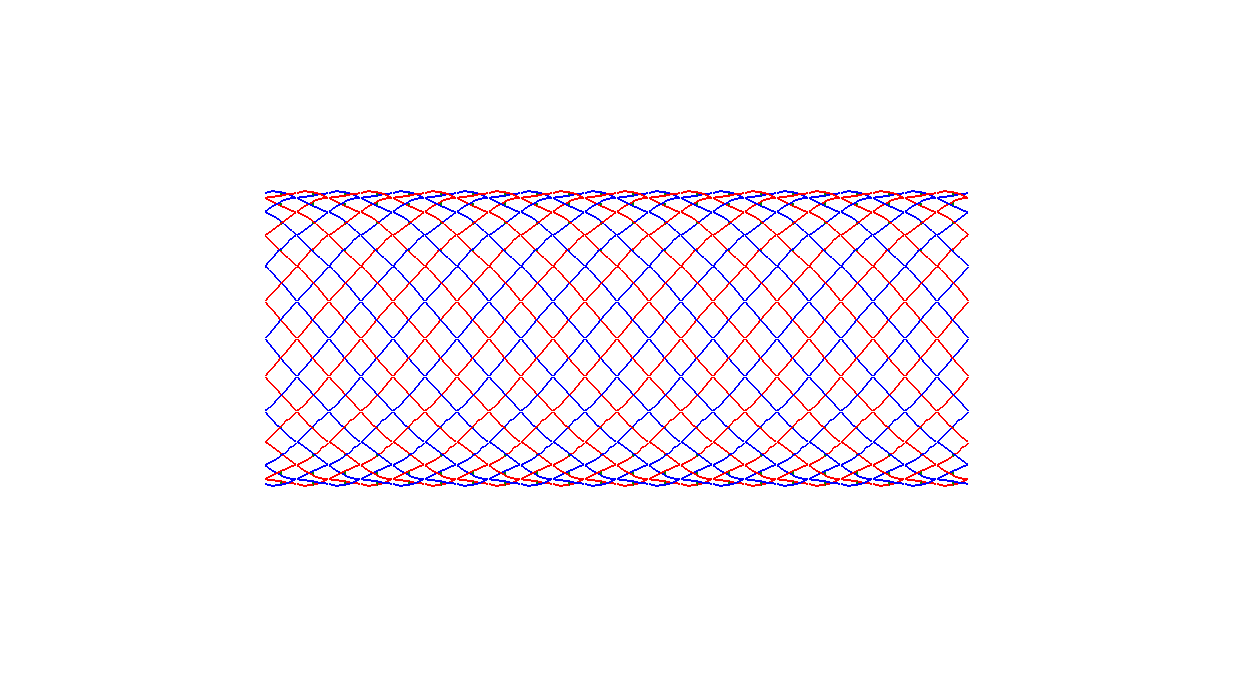
Full nearly planar pattern¶
The fully nearly planar pattern is obtained by copying the base module in two
directions and shown in Figure Full planar topology. replic2() generates this
pattern with 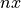 and
and 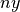 replications with steps
replications with steps 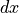 and
and
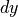 in respectively, the default X- and Y-direction.
in respectively, the default X- and Y-direction.
(lines 90-93)
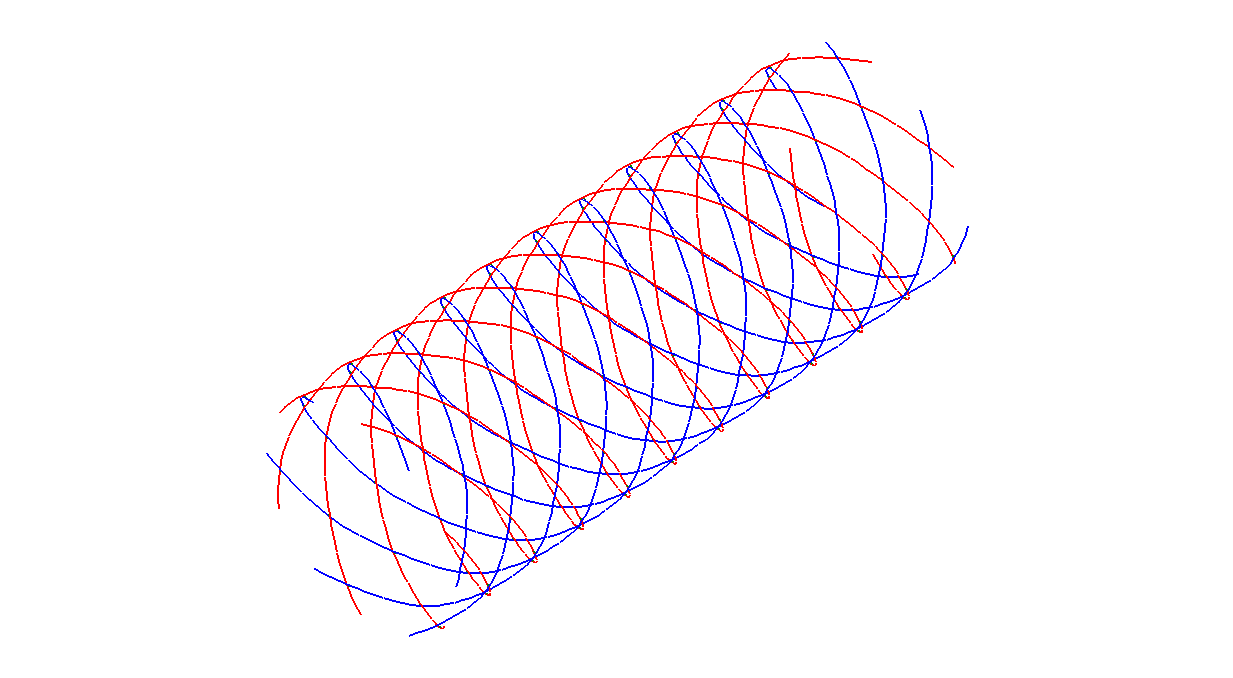
Cylindrical stent structure¶
Finally the full pattern is translated over the stent radius  in
Z-direction and transformed to the cylindrical stent structure by a coordinate
transformation with the Z-coordinates as distance
in
Z-direction and transformed to the cylindrical stent structure by a coordinate
transformation with the Z-coordinates as distance  , the X-coordinates
as angle
, the X-coordinates
as angle 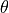 and the Y-coordinates as height
and the Y-coordinates as height  . The
. The
scale()-operator rescales the stent structure to the correct circumference
and length. The resulting stent geometry is depicted in Figure Cylindrical stent.
(lines 94-96)
In addition to the stent initialization, the DoubleHelixStent class script
contains a function all() representing the complete stent Formex.
Consequently, the DoubleHelixStent class has four attributes: the Formices
cell1, cell2 and all; and the number 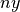 .
(lines 97-100)
.
(lines 97-100)
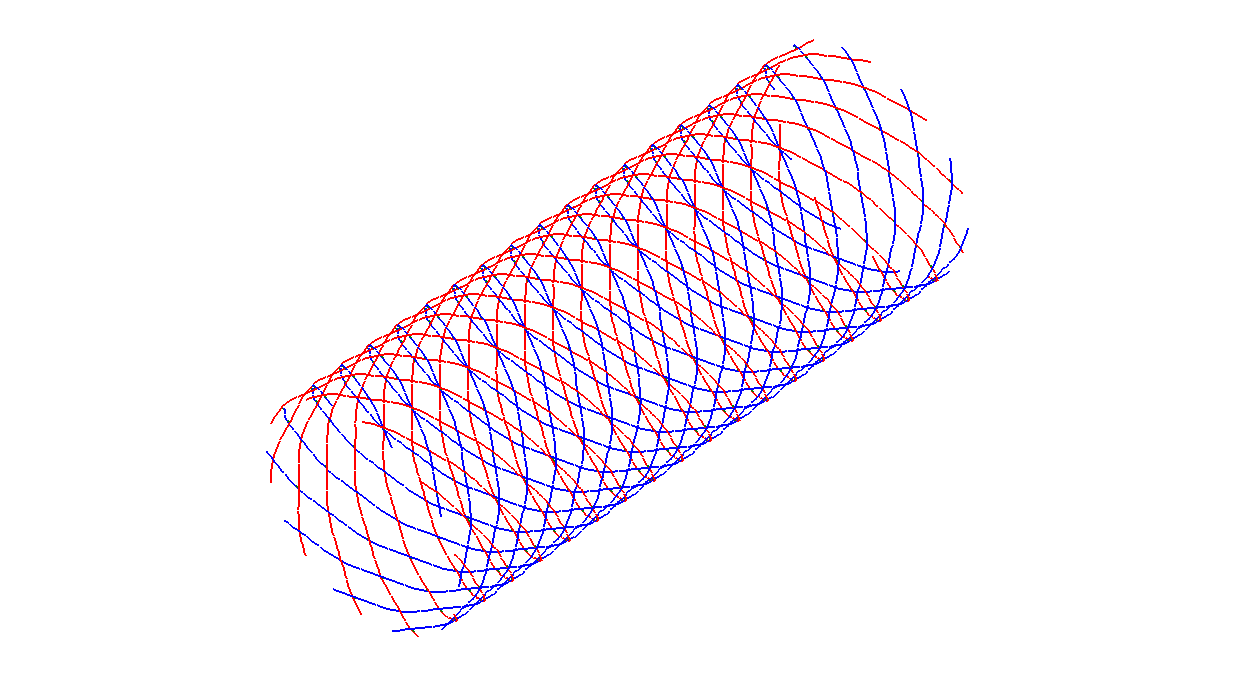
Parametric stent geometry¶
An inherent feature of script-based modeling is the possibility of easily
generating lots of variations on the original geometry. This is a huge advantage
for parametric analyses and illustrated in figures
Stent variant with De=16, nx=6, \beta=25: these wire
stents are all created with the same script, but with other values of the
parameters 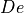 ,
, 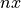 and
and 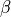 . As the script for building
the wire stent geometry is defined as a the
. As the script for building
the wire stent geometry is defined as a the DoubleHelixStent class in the
(WireStent.py) script, it can easily be imported for e.g. this purpose.
# *** pyformex ***
##
## This file is part of pyFormex 1.0.7 (Mon Jun 17 12:20:39 CEST 2019)
## pyFormex is a tool for generating, manipulating and transforming 3D
## geometrical models by sequences of mathematical operations.
## Home page: http://pyformex.org
## Project page: http://savannah.nongnu.org/projects/pyformex/
## Copyright 2004-2019 (C) Benedict Verhegghe (benedict.verhegghe@ugent.be)
## Distributed under the GNU General Public License version 3 or later.
##
## This program is free software: you can redistribute it and/or modify
## it under the terms of the GNU General Public License as published by
## the Free Software Foundation, either version 3 of the License, or
## (at your option) any later version.
##
## This program is distributed in the hope that it will be useful,
## but WITHOUT ANY WARRANTY; without even the implied warranty of
## MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
## GNU General Public License for more details.
##
## You should have received a copy of the GNU General Public License
## along with this program. If not, see http://www.gnu.org/licenses/.
##
from examples.WireStent import DoubleHelixStent
for De in [16.,32.]:
for nx in [6,10]:
for beta in [25,50]:
stent = DoubleHelixStent(De,40.,0.22,nx,beta).all()
draw(stent,view='iso')
pause()
clear()
Obviously, generating such parametric wire stent geometries with classical CAD methodologies is feasible, though probably (very) time consuming. However, as provides a multitude of features (such as parametric modeling, finite element pre- and postprocessing, optimization strategies, etcetera) in one single consistent environment, it appears to be the obvious way to go when studying the mechanical behavior of braided wire stents.
Operating on surface meshes¶
Besides being used for creating geometries, also offers interesting possibilities for executing specialized operations on surface meshes, usually STL type triangulated meshes originating from medical scan (CT) images. Some of the algorithms developed were included in .
Unroll stent¶
A stent is a medical device used to reopen narrowed arteries. The vast majority of stents are balloon-expandable, which means that the metal structure is deployed by inflating a balloon, located inside the stent. Figure Triangulated mesh of a Cypher® stent shows an example of such a stent prior to expansion (balloon not shown). The 3D surface is obtained by micro CT and consists of triangles.

Triangulated mesh of a Cypher® stent
The structure of such a device can be quite complex and difficult to analyse. The same functions offers for creating geometries can also be employed to investigate triangulated meshes. A simple unroll operation of the stent gives a much better overview of the complete geometrical structure and allows easier analysis (see figure Result of the unroll operation).
F = F.toCylindrical().scale([1.,2*radius*pi/360,1.])
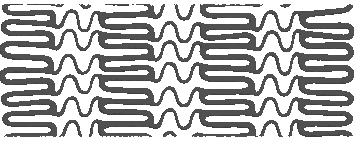
Result of the unroll operation
The unrolled geometry can then be used for further investigations. An important
property of such a stent is the circumference of a single stent cell. The
clip() method can be used to isolate a single stent cell. In order to obtain
a line describing the stent cell, the function intersectionLinesWithPlane()
has been used. The result can be seen in figures Part of the intersection with a plane.

Part of the intersection with a plane
Finally, one connected circumference of a stent cell is selected
(figure Circumference of a stent cell)
and the length() function returns its length, which
is 9.19 mm.

Circumference of a stent cell