strtox() and atox().
xatan2() and xreal::atan2().
The High Precision Arithmetic library (HPAlib) implements a high precision floating point arithmetic together with a comprehensive set of support functions. The general areas covered by these functions include:
The math library support includes evaluation of trigonometric, inverse trigonometric, hyperbolic, inverse hyperbolic, logarithm, and exponential functions at the same precision as the floating point math itself. The HPA library also supports high precision complex arithmetic and includes an Extended Precision Complex Math Library.
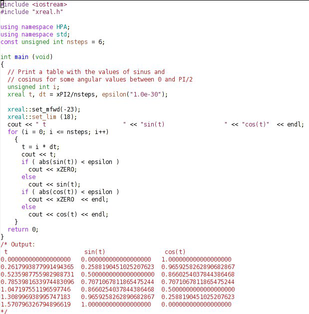
The last version of the HPA library comes with a C++ wrapper, which allows to perform high precision computations with the same syntax of the normal code.
The C and C++ languages define three types of floating point
numbers: if a programmer wants that a variable can store
not only integer values
but also values with a non-null fractional part, then he can
define this variable as a float, double or long double
variable.
If you are still reading this page, probably you know about
the usual binary representation of the numbers in the memory and
in the CPU of a computer. You know that it is possible
to represent only a limited range of numbers and that
non integer numbers are often approximated.
A non integer number could also have
a non periodic and infinitely long fractional part,
which has to be truncated to fit into the memory
of a computer: even if computers have nowadays
a big amount of memory, the storage space is still finite.
Probably you know that the difference between the three
floating point data types of C/C++ consists in the different range of
representable numbers and in the accuracy level which these numbers
are approximated with, if they can not be exactly represented
in binary notation.
Likely, you also know that each floating point data type has
an associated data size, which is given by the number of bytes
in the computer memory needed to store the
value of a variable of such data type.
According to the IEEE754 standard,
the size of a float variable is 4 bytes, the size
of a double variable is 8 bytes and the one of
a long double variable is at least 10 bytes,
even if the ANSI rules for C and C++ only require that
the size of a long double variable is
not less than that one of a double variable.
The general rule about the size of a floating point
data type is, that greater size implies a larger range
of representable values and higher accuracy in the
internal representation of the numbers.
Roughly speaking, the HPA library introduces a new floating point data type, which has a greater size (at least 16 bytes) and allows to represent a larger interval of numbers with an higher accuracy than the standard floating point data types.
The normal configuration of the library defines an extended floating point data type having a size of 16 bytes, which are so split:
The range of representable numbers is then given by
2^16384 > x > 2^[-16383] or
or
1.19*10^4932 > x > 1.68*10^-[4932].
The HPA library also defines an extended precision complex type, used to handle computations involving complex numbers. From the point of view of the HPA library, a complex number is simply a structure formed by two extended floating point numbers, representing respectively the real and the imaginary part of the complex number.
The accuracy provided by the extended floating point data type of the HPA library can be controlled by adjusting the size of its mantissa before compiling and installing the library. Normally, the size of the mantissa is equal to 7 words of 16 bits length, as told above. But it can be incremented by suitably setting the macro XDIM. XDIM defines the size of the mantissa of an extended floating point value in terms of words of 16 bits length. XDIM can take one of the following values: 7, 11, 15, 19, 23, 27, and 31. XDIM = 7 implies about 33 decimal digits of accuracy, XDIM = 31 about 149.
Once the HPA library has been built and installed, the size of its extended floating point data type can not be changed, unless you rebuild and reinstall the library. The HPA library does not supply the dynamic resizing of the numbers according to the currently requested precision and to the actual number of binary digits needed to represent a given value (numbers like 2.0 or 4.0 only need one digit of mantissa to be represented). If you are looking for similar features, then what you really want is an arbitrary precision arithmetic library, and you should look for it elsewhere, for example here.
The functions forming the HPA library are all implemented in a portable fashion in the C language. For values of XDIM not too large, they are quick enough. Even if there are no benchmarks, on an Intel Pentium(tm) I, 200 MHz, with 32 Mb of RAM (Operating system: NetBSD 2.0.2, compiler: gcc 3.3.3, optimization flags: -O3) and XDIM = 7 the suite of test programs distributed together with the library runs in a few seconds. For greater values of XDIM (>= 23 ) the overall performance of the routines of the library gets rapidly worse. For example, for XDIM = 31 and on the same machine as before the execution time for all test programs is about 3 minutes!
I plan to speed up the main routines of the library in the future releases, but unfortunately high precision arithmetic becomes too expensive when the mantissa of the extended floating point data type is very long. If you need an accuracy level much higher than the quadruple precision (XDIM=7), then the arbitrary precision approach is more convenient and you should look at http://gmplib.org/.
The Extended Precision Math Library is complete (or almost complete) both in its real and in its complex module: it includes trigonometric, inverse trigonometric, hyperbolic, inverse hyperbolic, logarithm, and exponential functions.
The HPA library and its C++ wrapper have been extensively tested. At the moment only a few weaknesses are known. They are listed in the BUGS file distributed together with the source code of the library. I think that the routines of HPAlib are quite reliable but I can NOT give you any warranty of that.
The C++ wrapper makes very simple to pass from double precision computations to extended precision ones. In most cases, the unique changes you will have to make to your C++ source code will be:
<xreal.h> (<xcomplex.h>)
at the head of your source file(s),
using namespace HPA;,
double (complex) data type with
xreal (xcomplex).
The library comes with a very detailed documentation (in English). Its programmer's manual, which is distributed together with the source code of the library, is available in the following formats:
Although the IEEE 754 standard for floating point hardware and software is assumed, HPAlib is not fully compliant to the IEEE 754 standard in what concerns the implementation of the quadruple precision.
The HPA library has been derived from a branch of the source code of the CCMath library, which is a work by Daniel A. Atkinson <DanAtk (at) aol (dot) com>. Since Daniel A. Atkinson released the code of the CCMath Library under GNU Lesser General Public License, I could modify, complete and redistribute this source code under the same terms.
The HPA (abbreviation of High Precision Arithmetic) Library is then copyrighted by me (Ivano Primi, <ivprimi (at) libero (dot) it>) and Daniel A. Atkinson. As for the CCMath Library, its source code is released under the terms of the GNU Lesser General Public License, as published by the Free Software Foundation; either version 2.1 of the License, or (at your option) any later version.
The HPA library is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU Lesser General Public License for more details.
You should have received a copy of the GNU Lesser General Public License along with this library; if not, see http://www.gnu.org/licenses/. Write to the email address
<ivprimi (at) libero (dot) it>
if you want to ask for additional information, report bugs or submit patches.
The tar-gzipped archive with the source code of the HPA library can be downloaded from
http://savannah.nongnu.org/download/hpalib
The last stable release of the HPA library is version 1.7. Together with the source code, the archive contains the full documentation (in English) of HPAlib. The manual is available in the following formats:
and can be browsed online here. Permission is granted to copy, distribute and/or modify this manual under the terms of the GNU Free Documentation License, Version 1.3 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled "GNU Free Documentation License". You can also obtain a copy of the GNU Free Documentation License from http://www.gnu.org/licenses/.
A big thanks to Daniel A. Atkinson, since without his work the HPA library would not exist. I have also to thank Aurelio Marinho Jargas <verde (at) aurelio (dot) net>, author of txt2tags (http://txt2tags.sf.net), a free (GPL'ed) and wonderful text formatting and conversion tool, which I used extensively in writing the programmer's manual of HPAlib and this web page.
Last but not least, I want to thank all the people till now involved in the Free Software community, starting from those ones directly involved in the GNU project (http://www.gnu.org).