This document provides a short introduction to the abstract ZigZag structure and gives some pointers for designing structures for various applitudes. Unlike most of the other documentation related to GZigZag, this document is more about the abstract structure, not this one particular implementation.
This introduction, even though it is short, is still rather technical and detailed and therefore the even gentler manuscript "GZigZag: a platform for Cybertext Experiments" is recommended to be read before this document.
This is work-in-progress: if there are any unclear parts, feel free to ask me to clarify things.
You are reading an ugly version of this document that doesn't use CSS to place floats nicely. Figures are shown in a very crude way. Get Mozilla and see the other version - it's MUCH better.
Introduction
The best words I've heard to describe the ZigZag structure are "hyperstructure kit". It is a set of tools or primitives for building hyperstructures. ZigZag was invented by Ted Nelson and is currently being implemented as a prototype at the University of Jyväskylä under the direction of the author. The purpose of this document is to introduce the reader to the ZigZag structure and some example applications of it.
This document was written using material and ideas from documents by and discussions with Ted Nelson, but also contains original ideas and material.
See also the glossary of ZigZag terminology in XXX.
Basics
To arrive at ZigZag from a general perspective, consider the problem of storing and visualizing information in a structure. Now, we naturally need some kind of ``atoms'', i.e.~indivisible pieces of information --- let's make an atom connected to a piece of text as the information it carries. Now, atoms should be connected to each other. Consider the two principles: 1) all connections must be two-directional and 2) to preserve visualizability, no cell should have an enormous number of connections. There are of course several different ways of realizing these principles but ZigZag is a particularly simple one.
ZigZag is a paradigm for manipulating data and devices, a platform if you may, in some way like UNIX. In UNIX (at least originally), everything is a file. Whether it is really a printer or the console or a network connection doesn't matter: the same basic operations (or at least a subset of them) is available. ZigZag is quite similar: everything is a cell and connections between the cells. However, the structure set up by ZigZag is far richer than a hierarchical file system, allowing more interconnectivity between related information.
|
|---|
All data in ZigZag consists of cells. A cell can contain e.g. text, an image or something like that --- basically, a unit of data. It does not matter how the content is stored; simply think of a cell as a little bit of data that has no significant internal structure (except of course the sequence for text, the places of the pixels for an image etc).
|
|---|
The cells are the primitives of the structure and the structure is formed
by connecting cells to each other through dimensions.
In each dimension, each cell can have one positive and one negative
neighbour. This means that all connections between cells are
two-directional: we speak of being neighbour to, or connected to,
not of linking to since linking nowadays means one-directional HTML-like
links.
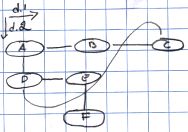
The different dimensions are denoted by names, such as d.1 or d.clone.
|
|---|
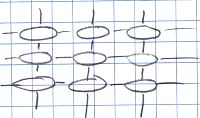
Now, if we have two dimensions and the cells are connected in a regular lattice, then this corresponds to a normal spreadsheet. However, no restriction is placed on which positive and negative ends are connected together - this is why this is called the ZigZag structure. All kinds of structures are possible: loops, spheres, trees etc. The kind of structure to choose for your application is up to your imagination.
|
|---|
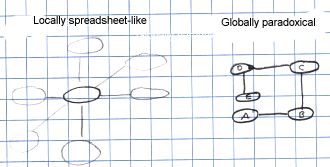
However, locally, from the perspective of one or two cells, this will still look like the spreadsheet: each cell has its neighbours and you go from it to one direction and then turn around and come back in the opposite direction, you end up in the same cell. So locally this structure is logical and simple --- like a spreadsheet --- but globally it is paradoxical: you can just keep going into one direction and arrive back where you came from, for example, or you can go left, down, right and up, and {\em not} come back where you started from in the end. This property gives more room in ZigZag for putting things in than a spreadsheet has, for instance.
One good way of visualizing this kind of structure is to think a device commonly found in science fiction books and films: a hallway with several doors. One door leads to a desert, and another to the antarctic. When you go through the door, you are in a different place but you can still walk back through the door, open the other door and walk through it. At each moment separately, you are operating under the rules of three-dimensional space known to us but when you pass the door and realize that you don't see the other door from the other side, you know that you are in a paradoxical environment.
Another place to look for good, related visualizations, is the work of M.C.Escher, who has created many paradoxical spaces that would fit well with ZigZag. However, not all of his paintings work this way: in ZigZag, directions are global: up is the same ``up'' everywhere, unlike in some of Escher's work, so care has to be taken with this analogy.
A slightly different way of looking at the structure that may sometimes help thinking about it is to consider dimensions as {\em labeled lists} of cells. That is, instead of considering cells and connections, consider lists (each list labeled with a string) of cells where the same cell may be on several lists (but only one with any given label). It is not difficult to see that this is exactly the same structure as above but viewed from a different angle: emphasizing the ranks instead of the single cell and its connections.
As an example of such a structure, consider a list of people and their birth years. It'd be quite natural to have first names, last names and birth years in their own columns, each row being one person. If done e.g.~on a spreadsheet, you would have to settle for the global rectangular structure. However, with ZigZag you can do more interesting things such as have the first names in alphabetical order, the last names in alphabetical order and finally even the birth years in numerical order in their own colums. This is because the columns are independent of each other, bound together simply by having the rows going across them. Displaying such a structure can be done in several different ways. Also, it would then be easy to select subsets of the people on other dimensions, for example for people who are currently in the same class or whatever.
It is useful to be able to see the structure from both perspectives since this will both help to overcome the feeling of paradoxicality from the spreadsheet-like connective picture but also remember that the cells are important objects in the list picture.
Comparing ZigZag with existing computer structures.
|
|---|
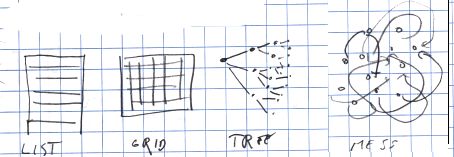
To put it coarsely, outside ZigZag there are three different kinds of structures in computers today: linear lists (and grids i.e.~lists of lists), hierarchical trees and messes. That is really messes, not meshes. By a mess, I mean any complicated data structure, usually with one-directional links to make things even more unmanageable.
The first two are inflexible, even with one-directional hierarchy-crossing links such as symlinks in filesystems or XML IDs. The third always requires much programming and debugging to do and is often hard to visualize.
ZigZag offers a fundamental new kind of structure where encoding new structures is simple because the coherence of the underlying simple flexible structure is guaranteed. At first it may seem strange that a structure that restricts the number of connections from each cell can be generic but this simple restriction is what brings about the coherence of ZigZag. In the sections below you'll see how this restriction does not prevent any structure from being represented using ZigZag but it enables several clever visualizations.
Among other things, ZigZag guarantees that there are no dangling pointers: all links are two-directional. You can always find which cells refer to a given cell.
One interesting thing to note about ZigZag and existing structures, the importance of which I really only realized while doing a demo at Nokia is simply that by using different dimensions, ZigZag allows you to arrange the same things into different traditional structures. So you can have the same cells in a tree along two dimensions (as you'll see below, trees are easiest done using two dimensions, one to go from the parent to the first child and the other to move along siblings), a list along another dimension and a table along two other dimensions. And possibly another tree in yet two more dimensions, if desired. If you use relcells (see below) you can even put the same things (this time, not cells: you do have to do a step of indirection) into different structures along the same dimensions.
Viewing
Now that the structure is defined, we have to be able to view and edit it on the computer somehow. Of course, we could just put this structure in a text file and edit it by naming cells with numbers and links by naming the cell numbers but this would lose the visuality inherent in the design.
There are many variations to the theme of viewing ZigZag structures. Views range from generic to specific views. Generic views are designed to be useful with a wide range of structures and usually therefore show only a small number of dimensions or a small number of steps along each dimension. Specific views on the other hand are free to do anything that suits the application at hand.
Specific views are related to applitudes, explained below in more detail.
In this section, we look at the structure of several generic views. Before going to the views themselves, let us first define some terms: the raster and the view. A raster is a way of selecting cells from the structure. A view is a way of placing the selected cells on the screen.
In order to look clear to the human observer, visual cues about the structure are vital. All neighbouring cells that lie next to each other should be connected with a line, and all cells that have neighbours that were not displayed because of the raster should have e.g. half of a connecting line, disappearing underneath the other cell in some visual fashion to show this. Also, when moving in the structure so that the part of
2D rectangular views
The 2D rectangular views are characterized by placing the cells in a spreadsheet-like rectangular grid on the screen. Even here, there are many different possible rasters for choosing which cells to place where, since a general ZigZag structure will not fit a rectangular grid and parts have to be clipped out. Note that the 2D here refers to the two-dimensionality of the rectangular grid, not that there need to be only two dimensions of the ZigZag structure showing. Usually we only have two in these views but as we see below, this is not a requirement.
The two simplest rasters useful for the rectangular views are the row and column rasters, which are actually the same raster but placed on the screen rotated 90 degrees from each other. These rasters are genuinely two-dimensional: they only use two dimensions in the ZigZag structure to find cells to display.
The row/column raster starts from the cursor and moves along one ZigZag dimension and place cells on the center column/row of the grid. After that column/row is full, the raster starts from the cells placed and from each, moves along the other dimension and places the cells found along the other dimension there.
These rasters are called hard rasters: the arrangement of cells is fixed so that there is only one possible path from the cursor to a cell to be placed in a given position on the screen. If there is no cell in the structure along such a path, then that location is left empty.
The converse of hard rasters are the soft rasters where there can be several different paths for each cell of the on-screen grid. The point of soft rasters is that since ZigZag structures are often relatively sparse in terms of connections, the hard row and column rasters may show relatively few cells at a time. Soft rasters are able to show more of the structure at the same time.
There are many different ways to define soft rasters for the rectangular grid. One fairly useful way is to specify the soft raster so that all the cells that a certain hard raster would show are shown, but additionally, if there is space left, more cells are shown along the dimensions.
Vanishing view
The vanishing view looks a little like the hard row/column raster above but is in fact a completely different beast. The raster for a vanishing view consists of all the cells within a given 2- or 3-dimensional Manhattan distance from the cursor (a Manhattan distance simply means the number of connections in any direction to get from one cell to another).
These cells are then placed on screen starting with the center cell and reducing the cell size as the distance from the cursor grows. This causes cells that would be in the same slot in the rectangular grid to be plotted apart from each other.
This could easily be generalized to more than three dimensions.
Compass view
The previous views have dealt with a few dimensions but several steps along those dimensions. The compass
Multicentric views
XXX
Text view
One simple view that can be easily overlooked is to simply take a rank of cells and show their texts appended to each other.
Applitudes
To distinguish itself from the traditional, monolithic applications, ZigZag uses the term applitude for a "zone of functionality". The difference between applications and applitudes is the interconnectivity: whereas conventional, monolithic applications are used to having all data in their own files, applitudes can easily share cells and simply use their own, orthogonal dimensions to connect cells.
The differences caused by this simple shift are enormous: instead of a selection of monolithic blocks, the contents of the computer can become an interconnected, organic whole. Everything connected to a particular person, for example, is connected to the same cell, whether in the email applitude, the calendar, the collection of documents or anything.
Designing structures
In this section, we'll go through some commonly occurring structural patterns in ZigZag. These can be thought of as being analogous to Design Patterns in Object-Oriented Programming. The patterns here are not formalized as far as OO design patterns but carrying out such a treatment would not be difficult.
As you will see, there are several different ways of encoding the same conceptual structure in ZigZag. The choice between using a different dimension or a rank of clones, for example. These alternative codings resemble in some way one of XML's similar ambiguities: for example whether to code something as an attribute or as a contained text-only element.
It is important to understand the difference between the low-level structure and the implied, higher-level structure. Single cells and single connections are building blocks, not necessarily complete entities by themselves.
Cloning
One of the basic structural mechanisms in ZigZag is
cloning, i.e. connecting cells on d.clone to imply that
they are somehow the same as the root clone, i.e. negend
of d.clone.
This mechanism is coupled with the cell content: the contents of all clones is the same as the contents of the root clone, and editing a clone edits the root clone.
XXX
There are alternatives to cloning, and in many cases they may be preferable. For instance, in a calendar applitude it would be possible to clone the cells for persons into the structures representing meetings but a possibly preferable approach would be to use an applitude-specific dimension for this. The reason is that then this dimension would always lead to predictable structure and the applitude could easily give interesting visualizations of the meetings a person participated or will participate in.
This is a fairly unsettled question. With more experience in designing different applitudes we will be able to tell easier when clones are appropriate and when special dimensions are better.
Arrangement along a dimension
Sometimes, there is a good, unique way of arranging cells along a dimension, e.g. alphabetical order. However, sometimes there is not, or there are two different orders you'd like to have.
This may seem like a difficult problem but actually, if all but one of the desired orders are easy to determine from the neighbours of the cells, then there is no problem at all: instead of expressing it directly in the structure, those orderings that are easy to construct algorithmically should be delegated to the view (as of yet, there are no viewers capable of this but they are under construction).
Another alternative (that does not currently work) will be
to thread the cells through several dimensions, most of which
are implicit: for example, an implicit d.1-alphabetic could
have the same ranks as d.1 but alphabetized. The implicit
dimensions would be read-only and be updated automatically
when the corresponding real dimensions changed.
If there is more than one order that is not easily determinable, then using two dimensions or cloning becomes a thing to consider.
Many to one reference
Even though the structure only allows only two connections along each dimension, it is possible for many cells to refer to one in ZigZag. This works by the way outlined above, by building a higher-level structure from the low-level building blocks of the cells and connections.
There are of course different ways for creating many to one reference, but two main ones distinguish themselves.
If the cell referred is very different from the cells referring to it, then a single rank, where the referred-to cell is the headcell is a good choice. Clones, for example, work this way (see above).
If the referents can be of the same "type", then it becomes necessary to allow the cell referred to to refer to another cell. In such case, a construction called a corner list is used. A corner list works by using two dimensions: the first one connects all the cells referring to a given cell and the second one connects the referred-to cell to the headcell of that rank. There are two main variants: the empty-headed one where the headcell is empty and the solid one where the headcell is one of the referring cells. The insert and delete referring cells operations are simpler for the empty-headed list since all referring cells are in the same position but that configuration wastes one cell.
Hierarchies
A hierarchy can be understood as a many-to-one reference relation, with the children of a given cell being the cells referring to it.
This would make a tree mapped as in the figure XXX.
It is good to remember that the same cells can be in several different trees using different dimensions.
Relation cells
Relation cells (relcells) are a commonly occurring construct in ZigZag. Fundamentally, relcells exist to declare a relationship between two cells or two groups of cells.
One example of a relcell would be the empty headcell in the empty-headed version of the corner list above. However, this is a fairly untypical example.
Typically, a relcell is on two or more ranks and implies a relationship between the headcells of those ranks. This way, each cell can have the same relationship to several other cells at the same time.
A good example of the use of a relation cell is the genealogy applitude (pardon the obvious puns). The idea is to connect all the siblings on one rank in the family tree and married couples on another, but this leaves open the question of representing the children born in the marriage. This is solved by placing a relcell between the parents, and hanging the sibling rank off that cell as the headcell. This relcell then implies a parent-child relationship between the cells connected to it..
Designing easily versionable structures
Moved from DesignProblems; not yet edited to fit in.
Versioning and merging has important implications for structural design.
|
|---|
For example, it provides (XXX image) a good reason to use blank cells in corner lists for separating the parent and sibling relationships. Consider the situation where the ordering of the siblings is changed by two people independently. Merging in this change with the blank cell is straightforward: it is simply changing the arrangement of a single rank, with the headcell remaining in place.
If the headcell is one of the sibling cells, however, then merging has to be done simultaneously for the two relations on it: the cell that is the headcell in the final version must be the cell on the parent-child rank.
Of course, this same reasoning also applies to plain editing of the structure using hop: the corner lists without the blank cell are often clumsy because the one cell is overloaded with two functions. Hmm... this may be a key insight to something important...
The existence of this "problem" is fairly natural. The blank cell is most certainly not without a purpose: it is the identity cell of the list. We seem to be using too few identity cells in our structures.
An identity cell is absolutely essential for any part of the structure that should be referable. As every object (structure) has its own invariants, the only thing we can assume in general is a permanent identity cell. In addition to being required, the identity cell is also sufficient for any referral.
![]() The problem here was that the parent referred to a specific
element of the list, not the list itself; that would have been
impossible, as the list had no identity cell. Without the id cell,
there is no way of knowing who refers to the list and who to the
first element, so we don't even need versioning to get some really
big problems. The best we can do without identity cells for lists
is referral to "the list this cell is on along dimension x".
The problem here was that the parent referred to a specific
element of the list, not the list itself; that would have been
impossible, as the list had no identity cell. Without the id cell,
there is no way of knowing who refers to the list and who to the
first element, so we don't even need versioning to get some really
big problems. The best we can do without identity cells for lists
is referral to "the list this cell is on along dimension x".
![]() I agree to this. However, I don't understand where you go from
here: I would simply conclude here that identity cells
are a good idea...
I agree to this. However, I don't understand where you go from
here: I would simply conclude here that identity cells
are a good idea...
![]() Referrals to "the list this cell is on along dim x", or "the cell
three cells posward on
Referrals to "the list this cell is on along dim x", or "the cell
three cells posward on d.myway, then four on d.highway" are not
referrals to the structure, and thus do not have identity cells.
What would an identity cell for the first of these referrals be,
if there were one? That would of course be the list itself, but it
is not a "list with this particular cell", it is just a list. Thus
the target of referral does not exist in the structure.
![]() As the same cell can't denote the query and the reply (except in
trivial cases), a level of indirection is needed. We can use a
connection that automatically points to the right cell (using
either a space part or a trigger), or we can create an identity
cell for an expression (the query, as e.g. a Clang expression, or a
cell with an automatic connection) referring to the right cell
(the reply). An id cell has the benefit that it can be referred
to; on the other hand, the connection may be transparently
inserted into structures. Using a space part for the connection
is possible only if space parts are allowed to manage connections
along "normal" dimensions between two possibly normal cells.
As the same cell can't denote the query and the reply (except in
trivial cases), a level of indirection is needed. We can use a
connection that automatically points to the right cell (using
either a space part or a trigger), or we can create an identity
cell for an expression (the query, as e.g. a Clang expression, or a
cell with an automatic connection) referring to the right cell
(the reply). An id cell has the benefit that it can be referred
to; on the other hand, the connection may be transparently
inserted into structures. Using a space part for the connection
is possible only if space parts are allowed to manage connections
along "normal" dimensions between two possibly normal cells.
![]() What does this mean? 1. Why do you want to refer to something
like that? 2. why does a clang subroutine not work there?
The structure needn't be able to do everything.
Note that if you want to speculate on the mathematical
details of things, you should probably start a new document
for that; this document is meant to be practical.
What does this mean? 1. Why do you want to refer to something
like that? 2. why does a clang subroutine not work there?
The structure needn't be able to do everything.
Note that if you want to speculate on the mathematical
details of things, you should probably start a new document
for that; this document is meant to be practical.
![]() 1. The only use for this that I've come up with is insertion of
results of database-like queries into ZZ structures. 2. It works,
but it's not a solution to the (irrelevant?) problem.
1. The only use for this that I've come up with is insertion of
results of database-like queries into ZZ structures. 2. It works,
but it's not a solution to the (irrelevant?) problem.
![]() Space parts can also be used to define new structures
based on a space, iff there is a surjection from the valid
states of the space to the valid space part states. If
the space part is to be writable (user can change from any
valid space part state to any other), the surjection must
also be an injection. Note that any connections to space part
cells are part of the space, and such connections are very
likely to reduce the number of valid space states due to
unpredictably changing space part cell id's. The most relevant
definition for valid space states is "makes sense to the user",
and wildly breaking and moving connections usually don't make any
sense.
Space parts can also be used to define new structures
based on a space, iff there is a surjection from the valid
states of the space to the valid space part states. If
the space part is to be writable (user can change from any
valid space part state to any other), the surjection must
also be an injection. Note that any connections to space part
cells are part of the space, and such connections are very
likely to reduce the number of valid space states due to
unpredictably changing space part cell id's. The most relevant
definition for valid space states is "makes sense to the user",
and wildly breaking and moving connections usually don't make any
sense.
Example applitudes
XXXThe Cousin Problem
There is one important problem when dealing with data that has relations, which the author calls the "Cousin" problem. Consider the genealogy applitude. Now, insert a new person, A, and then his cousin, B. A moment's reflection will show that this is impossible in the data structure explained above.
This is because in the human representation of concepts, there is no hierarchy between mother, father, son, daughter and cousin. There is no good way to pick just one way to represent the information since the idea "B is A's cousin" is perfectly valid, even without knowing whether it is on the mother's or father's side.