Linear Algebra

GSL Shell has moved

The project, its documentation and the release packages are now hosted on Github. Please find here the user manual.

Functions

GSL Shell gives access to some functions of linear algebra based on GSL itself or on the BLAS routines.

matrix.inv(m)

Returns the inverse of the matrix m.

matrix.solve(A, b)

Solve the square system A x = b where A is a square matrix, b is a column matrix. It returns the solution x of the system.

matrix.svd(m)

A general rectangular M-by-N matrix A has a singular value decomposition (SVD) into the product of an M-by-N orthogonal matrix U, an N-by-N diagonal matrix of singular values S and the transpose of an N-by-N orthogonal square matrix V,

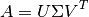
The singular values σ_i = Σ_ii are all non-negative and are generally chosen to form a non-increasing sequence σ₁ >= σ₂ >= ... >= σ_N >= 0.

The singular value decomposition of a matrix has many practical uses. The condition number of the matrix is given by the ratio of the largest singular value to the smallest singular value. The presence of a zero singular value indicates that the matrix is singular. The number of non-zero singular values indicates the rank of the matrix. In practice singular value decomposition of a rank-deficient matrix will not produce exact zeroes for singular values, due to finite numerical precision. Small singular values should be edited by choosing a suitable tolerance.

For a rank-deficient matrix, the null space of A is given by the columns of V corresponding to the zero singular values. Similarly, the range of A is given by columns of U corresponding to the non-zero singular values.

Note that the routines here compute the “thin” version of the SVD with U as M-by-N orthogonal matrix. This allows in-place computation and is the most commonly-used form in practice. Mathematically, the “full” SVD is defined with U as an M-by-M orthogonal matrix and S as an M-by-N diagonal matrix (with additional rows of zeros).

This function returns three values, in the order, U, Σ, V. So you can write something like this:

u, s, v = svd(m)