Step 1
Plug in the first progression:
4, 3364, 6724

Step 2
Plug in another progression:
9409, 12769, 16129

Step 3
Find the equidistant point.

A magic square is where the the rows, columns and main diagonals add up to the same number. They come in all sizes, but the smallest possible magic square is 3x3 -- and these are very easy to find. However, a 3x3 magic square containing only perfect squares has never been found.
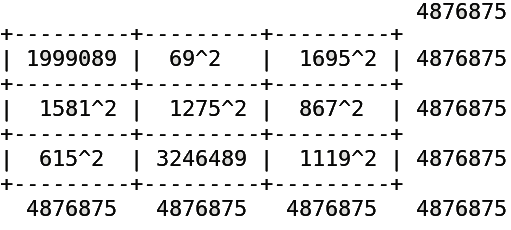
The closest magic square of squares was found by Andrew Bremner in 1997, and it contains seven of nine perfect squares:
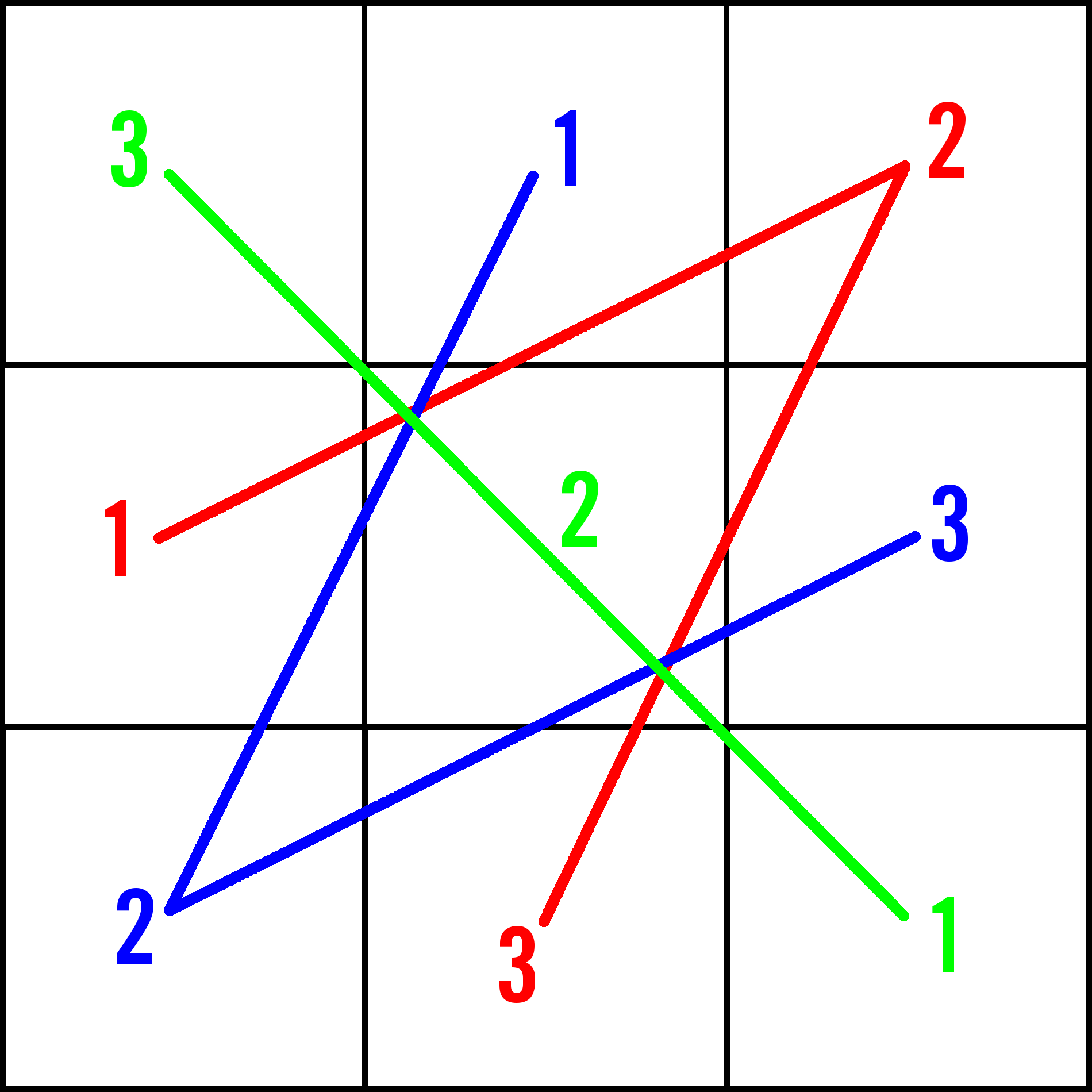
The structure of it is shown in red, blue and green lines on the left.
It is comprised of three arithmetic progressions that have the same
distance between the numbers. In this case the distance is:
615^2 - 69^2 = 378225 - 4761 = 373464
A 3x3 magic square of nine perfect squares will contain three arithmetic progressions (e.g. red, green, and blue), where each of the values are perfect squares and they have the same distance between their values.
To find the elusive 3x3 magic square of squares, we have to search for collections of arithmetic progressions of perfect squares that have the same distance. But there are a finite number of pairs of perfect squares that have a given distance. This can be illustrated with this triangle of square differences:
0,
3,
8, 5,
15, 12, 7,
24, 21, 16, 9,
35, 32, 27, 20, 11,
48, 45, 40, 33, 24, 13,
63, 60, 55, 48, 39, 28, 15,
80, 77, 72, 65, 56, 45, 32, 17,
99, 96, 91, 84, 75, 64, 51, 36, 19,
120, 117, 112, 105, 96, 85, 72, 57, 40, 21,
143, 140, 135, 128, 119, 108, 95, 80, 63, 44, 23,
168, 165, 160, 153, 144, 133, 120, 105, 88, 69, 48, 25,
195, 192, 187, 180, 171, 160, 147, 132, 115, 96, 75, 52, 27,
224, 221, 216, 209, 200, 189, 176, 161, 144, 125, 104, 81, 56, 29,
255, 252, 247, 240, 231, 220, 207, 192, 175, 156, 135, 112, 87, 60, 31,
288, 285, 280, 273, 264, 253, 240, 225, 208, 189, 168, 145, 120, 93, 64, 33,
323, 320, 315, 308, 299, 288, 275, 260, 243, 224, 203, 180, 155, 128, 99, 68, 35,
360, 357, 352, 345, 336, 325, 312, 297, 280, 261, 240, 217, 192, 165, 136, 105, 72, 37,
399, 396, 391, 384, 375, 364, 351, 336, 319, 300, 279, 256, 231, 204, 175, 144, 111, 76, 39,
This triangle contains the difference of one perfect square with every other perfect square. There are twenty rows, and nineteen columns.
The value 3 is the difference between the squares 4 and 1. The value 8 is the difference between 9 and 1. The value 5 is the difference between 9 and 4.
3 is the result of subtracting the 2nd square (in the infinite list of perfect squares, which is 4) from the 1st square (which is 1). The cool thing about this triangle is that the row and column encodes this information: 3 is on the 2nd row and 1st column.
Let's try it again with 19:
You will notice that 19 doesn't appear again after that. Some numbers get repeated many times in this triangle, but poor old 19 only has one instance. When a row ends in a number that is bigger than the difference we're looking for, it is guaranteed to not appear afterwards -- there is no use in searching any further because there isn't another pair of perfect squares that have that difference.
Why does this matter? Because it is identifying a pair of perfect squares for a given difference. And if you have two of these pairs in the right configuration, you have an arithmetic progression of three perfect squares. (We know that an arithmetic progression of four perfect squares is impossible.) And if we have three of these progressions (red, blue, and green) in the right configuration, we will have a 3x3 magic square of squares!
One number that appears many times in the triangle of square differences is 3360. It appears 16 times in total.

Instead of showing the myriad of numbers here, all numbers are represented with a tiny #, except for 3360 which is represented by a blank.
There are more instances of 3360 that aren't shown here (11 are shown with 5 not shown), but the curve continues on. When the curve hits the side of the triangle, we're out of possibilities for more hits on 3360.
Here are the points that 3360 occupies in the triangle:
col row 2, 58 -> 3360 = 3364 - 4 = (58 * 58) - (2 * 2) 11, 59 -> 3360 = 3481 - 121 = (59 * 59) - (11 * 11) 19, 61 -> 3360 = 3721 - 361 = (61 * 61) - (19 * 19) 22, 62 -> 3360 = 3844 - 484 = (62 * 62) - (22 * 22) 41, 71 -> 3360 = 5041 - 1681 = (71 * 71) - (41 * 41) 46, 74 -> 3360 = 5746 - 2116 = (74 * 74) - 46 * 46) 58, 82 -> 3360 = 6724 - 3364 = (82 * 82) - (58 * 58) 74, 94 -> 3360 = 8836 - 5475 = (94 * 94) - (74 * 74) 97, 113 -> 3360 = 12769 - 9409 = (113 * 113) - (97 * 97) 113, 127 -> 3360 = 16129 - 12769 = (127 * 127) - (113 * 113) 134, 146 -> 3360 = 21316 - 17956 = (146 * 146) - (134 * 134) 163, 173 -> 3360 = 29929 - 26569 = (173 * 173) - (163 * 163) 206, 214 -> 3360 = 45796 - 42436 = (214 * 214) - (206 * 206) 277, 283 -> 3360 = 80089 - 76729 = (283 * 283) - (277 * 277) 418, 422 -> 3360 = 178084 - 174724 = (422 * 422) - (418 * 418) 839, 841 -> 3360 = 707281 - 703921 = (841 * 841) - (839 * 839)
But this list is only pairs of squares, when we want three in a row, e.g. an arithmetic progression of three perfect squares. An easy way to find them in this list is to see if a value is shared between our row and columns. For example, we can see that 58 appears twice, and so does 74, and 113. This means 3360 yields three arithmetic progressions with the same distance! Only 6 of the 16 instances of 3360 in the triangle of square differences were usable.
Here are the three arithmetic progressions that have a distance of 3360.
4, 3364, 6724,
2116, 5476, 8836,
9409, 12769, 16129,
Some special numbers have hundreds and thousands of instances in the triangle of square differences, and can yield hundreds of arithmetic progressions containing three squares. You can see why too -- the height and width of that curve only grows as the number we're searching for gets larger. There is a portion of the triangle at the top that does not involve the curve at all, and as we saw earlier, there is an end to the curve too (when it intersects with the slanted triangle line). But the height and width of it only grows as we go deeper into the triangle.
We only need three arithmetic progressions of perfect squares to make a 3x3 magic square of squares, and 3360 has given us three, but these particular progressions do not work together to give us the elusive 3x3 magic square of squares.
Let's plug them in and see why. This is what we call the scissor configuration.
Step 1
Plug in the first progression: 
|
Step 2
Plug in another progression: 
|
Step 3
Find the equidistant point. 
|
Well that half integer can't work! We can multiply any perfect square by any other square larger than one to get another square. This scales our progressions so we don't have any half integers.
Step 4
Multiply by 4. 
|
Step 5
Fill in the rest of the numbers. 
|
DoneAdd up the rows, columns, and diagonals. 
|
Our red and blue progressions worked fine, but unfortunately they didn't shake out any other perfect squares on the diagonal line. This magic square has 6 perfect squares, which is pretty good, considering only one square with seven has ever been found. The hope is that someday the diagonal green progression will shake out as all perfect squares, or at least one more square.
We can try again, plugging in the progressions differently, in what we call the warbird configuration.
Step 1
Plug in the first progression: 
|
Step 2
Plug in the another progression: 
|
Step 3
Fill in the rest. 
|
We have created another magic square with the red and green progressions but none of the other numbers shook out as perfect squares, so it only has six squares in total.
We have illustrated how any two arithmetic progressions of three perfect squares with the same distance can create a 3x3 magic square with at least six perfect squares. And what's more, we can make two different magic squares (with two different magic numbers). We have also illustrated how there are a finite number of progressions with a given distance, but simultaneously there are an infinite number of possibilities.
If you can discover a fast way to find these progressions, that are very large (like 10^30) and have the same distance between them, you will be on the cutting edge of the search for the elusive 3x3 magic square of squares.
As we find more arithmetic progressions, we have to try every combination of two to see if a seventh, eighth, or ninth perfect square shakes out, in both the scissor and warbird configurations. In the Fituvalu software, the scissor-square program does this.
But all this is just one approach to make a magic square of squares. Another approach is Lee Morgenstern's way to create 3x3 magic squares from arithmetic progressions with different distances, but have a perfect square in common. They make magic squares with five or more perfect squares. In Fituvalu, this is the 3sq-pair-search program. To use Morgenstern's method to create magic squares from parametric values use morgenstern-search-type-1, etc.
Lastly, magic squares can have multiples, rotations, and reflections.
If we multiply any magic square by 4 (or any other perfect square), we will have another magic square. But this isn't really a new magic square. The relations between the numbers are the same, and it will never magically contain a seventh perfect square in it. Rotations and reflections are self-explanatory. In Fituvalu, the unique-squares program takes multiples, rotations and reflections into account, and discards all but the unique magic squares.
Copyright (C) 2017 Ben Asselstine
This page is licensed under the terms of the Creative Commons Attribution ShareAlike 4.0 Intl License.
Go back to Fituvalu.
